 |
|
Основное уравнение динамики вращательного движения, момент силы, момент инерции
Пусть к материальной точке массы m приложена сила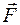 
. Моментом силы 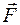относительно оси вращения называют вектор, определяемый формулой
.
Модуль этого вектора равен
, 
,
где 
– составляющая силы в плоскости, перпендикулярной к оси вращения, 
– вектор, проведенный от оси вращения к материальной точке (рис. 11, ось вращения проходит через точку О перпендикулярно к вектору ), 
– плечо силы (кратчайшее расстояние от линии действия силы до оси вращения). Вектор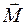 
направлен вдоль оси вращения.
Для абсолютно твердого тела, представляющего собой совокупность материальных точек массами dm, помимо векторной суммы моментов внешних сил 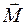, действующих на его материальные точки, между материальными точками этого тела действуют также и внутренние силы. Однако согласно третьему закону Ньютона векторная сумма моментов внутренних сил относительно оси вращения равна нулю, и поэтому
.
|
| Рис. 11. Маятник Обербека |
В итоге основной закон динамики вращательного движения для абсолютно твердого тела представляется в виде
 ,
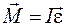| (1) |
который формулируется следующим образом:
произведение момента инерции тела относительно оси вращения на вектор углового ускорения равно векторной сумме моментов действующих на тело внешних сил относительно этой оси вращения.
Сравнивая (1) с выражением второго закона Ньютона для поступательного движения 
, можно заключить, что при вращательном движении роль силы F выполняет момент силы M, роль массы m – момент инерции I. Следовательно, момент инерции является мерой инертности вращающегося тела.
Маятник Обербека
Для проверки законов вращательного движения в данной работе используется маятник Обербека, схема которого изображена на рис. 11.
Маятник Обербека состоит из четырех стержней 2, укрепленных на втулке под прямым углом друг к другу. На стержнях закрепляются грузы 1, перемещая которые, можно менять момент инерции тела. На одной оси с маятником находится шкив 3 радиусом r. Гиря 4, приводящая тело во вращение, прикреплена к концу нити, которая наматывается на шкив 3. На основную гирю массой m могут надеваться дополнительные грузы массой 
.
Если на барабан, вращающийся относительно оси, проходящей через точку O, намотать шнур с привязанным к его концу грузом массы m, то, будучи представлена самой себе, система придет в ускоренное движение.
Изменяя массу груза, подвешенного к нити, можно изменить вращающий момент сил. Перемещая грузы 2 вдоль стержней, можно менять момент инерции системы.
На груз будут действовать две силы: сила тяжести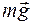 
и натяжение нити 
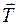. Второй закон Ньютона для груза в проекции на ось, совпадающей с нитью будет иметь вид:
 ,
|
отсюда
 .
| (2) |
Ускорение груза a можно определить из законов кинематики, измеряя время t, за которое груз опустится на величину h, имея начальную скорость 
по формуле
 ,
|
или
 .
| (3) |
Подставляя (3) в (2), найдем силу натяжения нити
 .
| (4) |
Если радиус барабана r, то натянутая нить создает вращающий момент
 .
| (5) |
Тогда основное уравнение динамики вращательного движения твердого тела (без учета сил трения) будет иметь вид
или
 .
| (6) |
Заменяя T из (4), получим
 .
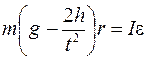| (7) |
Все точки барабана имеют одинаковое угловое ускорение ε. Точки, лежащие на ободе барабана, обладают касательным ускорением 
, равным ускорению груза a, т.к. нить нерастяжима, поэтому можно записать
 .
| (8) |
Подставляя (8) в (7) с учетом (3), получим
 .
|
Используя уравнения (4) и (5) можно записать
 .
| (9) |
Из (8) с учетом (3) под действием этого момента сил M маятник Обербека вращается с угловым ускорением
 .
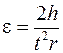| (10) |