Индивидуальные задания:

По 14 предприятиям отрасли исследуется зависимость производительности труда (у), (т/час) от уровня механизации работ (x₁) (%),среднего возраста работников (лет) (x₂) и энерговооруженности труда (x₃) (КВт/100 работающих). Провести корреляционный анализ. Отчет представить преподавателю. Данные по предприятиям приведены в таблице 16.

Рисунок 12

Таблица 16

Вариант 1 x1 32 30 36 40 41 47 56 54 60 55 61 67 69 76 x2 33 31 41 39 46 43 34 38 42 35 39 44 40 41 x3 30 29 35 40 40 48 50 52 59 54 60 70 70 75 y 20 24 28 30 31 33 34 37 38 40 41 43 45 48	Вариант 2 x1 55 46 40 39 35 29 31 75 68 66 60 54 59 53 x2 33 42 45 38 40 30 32 40 39 43 38 34 41 37 x3 50 45 39 40 34 30 30 74 69 66 59 54 60 52 y 33 32 30 29 27 23 19 47 44 42 40 39 37 36
Вариант 3 x1 48 57 55 61 56 62 68 70 77 42 41 37 31 33 x2 44 35 39 43 36 40 45 41 42 47 40 42 32 34 x3 47 56 54 62 56 62 67 70 76 42 40 37 30 32 y 34 35 38 39 41 42 44 46 49 32 31 29 25 21	Вариант 4 x1 52 54 45 39 38 34 28 30 74 67 65 59 53 58 x2 36 32 41 44 37 39 29 31 39 38 42 37 33 40 x3 52 53 45 38 38 34 28 31 73 66 65 60 52 57 y 35 32 31 29 28 26 22 18 46 43 41 39 38 36
Вариант 5 x1 43 49 58 56 62 57 63 69 71 78 34 32 38 42 x2 48 45 36 40 44 37 41 46 42 43 35 33 43 41 x3 42 48 58 55 61 56 62 70 70 78 35 32 38 41 y 33 35 36 39 40 42 43 45 47 50 22 26 30 32	Вариант 6 x1 52 57 51 53 44 38 37 33 27 29 73 66 64 58 x2 32 39 35 31 40 43 36 38 28 30 38 37 41 36 x3 52 56 50 53 45 37 37 32 28 30 72 66 64 59 y 37 35 34 31 30 28 27 25 21 17 45 42 40 38
Вариант 7 x1 39 43 44 50 59 57 63 58 64 70 72 79 35 33 x2 44 42 49 46 37 41 45 38 42 47 43 44 36 34 x3 45 42 50 46 38 40 45 39 41 48 43 44 35 34 y 31 33 34 36 37 40 41 43 44 46 48 51 23 27	Вариант 8 x1 63 57 51 56 50 52 43 37 36 32 26 28 72 65 x2 40 35 31 38 34 30 39 42 35 37 27 29 37 36 x3 39 38 35 35 32 31 28 28 25 25 21 15 45 40 y 39 37 36 34 33 30 29 27 26 24 20 16 44 41
Вариант 9 x1 64 59 65 71 73 80 36 34 40 44 45 51 60 58 x2 46 39 43 48 44 45 37 35 45 43 50 47 38 42 x3 50 40 50 55 50 60 35 34 42 41 48 49 50 50 y 42 44 45 47 49 52 24 28 32 34 35 37 38 41	Вариант 10 x1 46 52 61 59 65 60 66 72 74 81 37 35 41 45 x2 51 48 39 43 47 40 44 49 45 46 38 36 46 44 x3 46 52 60 58 64 61 65 72 74 80 38 34 40 44 y 36 38 39 42 43 45 46 48 50 53 25 29 33 35

Лабораторная работа 7.

Регрессионный анализ в ППП STATISTIСА

Цель работы: Изучить возможности ППП STATISTIСА для проведения многофакторного регрессионного анализа.

УСЛОВИЕ ЗАДАЧИ.

По 20 предприятиям отрасли изучается зависимость выработки продукции на 1 работника(у), тыс.руб. - "ВЫРАБОТКА" от ввода в действие новых основных фондов в % от стоимости фондов на конец года (х1) "ФОНДЫ'' и от удельного веса рабочих высокой квалификации в общей численности рабочих (х2), % - "РАБОЧИЕ". Исходные данные представлены на рис.13.

Рисунок 13Исходный файл с данными

Задания:

1. Получить описательные статистики по каждому признаку. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения метода наименьших квадратов для их изучения.

2. Составить уравнение множественной регрессии, оценить его параметры пояснить их экономический смысл.

3. Проанализировать линейные коэффициенты парной и частной корреляции.

4. Оценить значения скорректированного и нескорректированного линейных коэффициентов множественной корреляции.

5. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии в целом.

Решение задачи

1. Для получения описательных статистик необходимо в Переключателе модулей (см.рис.14), появившемся после запуска пакета STATISTICА, выбрать команду Basic Statistics/Tables, при этом на экране появится стартовая панель модуля Основные статистики и таблицы (Basic Statistics/Tables), в которой следует выбрать команду Descriptive statistics. Если файл с данными создан заранее, то статистическую обработку данных следует предварить открытием уже существующего файла с данными через команду Open Data (рис.14), или предварительно создать новый файл данных (внести данные в таблицу и сохранить). Выбрав команду ОК, на экране появятся окно Descriptive statistics (рис.15), выберите закладку Advanced и настройте параметры как показано на рисунке, затем дайте команду Summary.В появившемся окне выберите переменные 1-3 и команду ОК. На экране появятся описательные статистики (рис.16), анализ которых следует начать с определения показателей вариации.

Рисунок 14 Стартовая панель модуля Основные статистики и таблицы

Рисунок 15 Окно настройки параметров модуля Описательные статистики

Рисунок 16 Результаты работы модуля Описательные статистики

Сравнивая значения средних величин (графа Mean, рис.16) и средних квадратических отклонений (графа Standard deviation, рис.16), определим коэффициент вариации как их отношение (Vy = 25,6 %, Vx₁=31,3%, Vx₂=30,6%), приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 33%. Значения коэффициентов асимметрии (графа Skewness, рис.16), эксцесса (графа Kurtosis, рис.16) не превышают двухкратных среднеквадратических ошибок (графы Standard error of skewness, Standard error of kurtosis, рис.16). Это указывает на отсутствие значимой скошенности и остро-(плоско) вершинности фактического распределения предприятий по значениям каждого признака по сравнению с их нормальным распределением.

Вывод: совокупность предприятий однородна и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

2. Для построения уравнения множественной регрессии необходимо в меню Statistics выбрать модуль Multiple Regression. При этом на экране появится окно Muliple Linear Regression. После выбора команды Variable, следует указать зависимую (ВЫРАБОТКА) и независимые переменные (ФОНДЫ, РАБОЧИЕ) и нажать ОК. После чего появится окно Multiple Regression Results (рис.17).

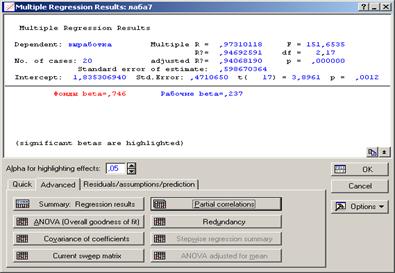
Рисунок 17 Панель вывода результата модуля Множественная регрессия

Выбрав команду Summary: Regression results, получаем результаты работы модуля МНОЖЕСТВЕННАЯ РЕГРЕССИЯ (рис.18) на основании которых строим уравнение линейной множественной регрессии. Свободный член и коэффициенты регрессии представлены в графе В (рис.18) a₀=1,835; а₁=0,946; а₂=0,086. При этом уравнение множественной регрессии примет вид: y =1,835+0,946*х₁+ 0,086*x₂.

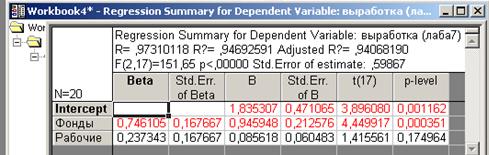
Рисунок 18 Результаты построения множественной линейной регрессионной модели

Для оценки значимости полученных коэффициентов регрессионного уравнения воспользуемся t-критерием Стьюдента (графа t(17), рис.18). В пакете STATISTICA значения t-критерия (t_p) определяются как отношение взятого по модулю коэффициента регрессии (графа В, рис.18) к его стандартной ошибке (графа St. Err. of В, рис.18). Табличное значение t-критерия с уровнем значимости α=0,01 и числом степеней свободы d.f.=n-m-1=17 составляет: t_T =2,89 (прил.1). Сравним значения t_p и t_T для каждого из полученных параметров:

t_p =3,89> t_T - для свободного члена a₀;

t_p =4,44> t_T - для коэффициента a₁;

t_p =1,41< t_T - для коэффициента а₂.

Таким образом, статистически значимыми являются коэффициенты a₀ и a₁ а коэффициент а₂ сформирован под влиянием случайных причин. Поэтому фактор х₂ можно исключить из модели как неинформативный. Аналогичный вывод можно сделать, сравнивая значения уровня значимости (графаp-level, рис. 18) с принятым нами уровнем α=0,01. Для a₀ и a₁ показатель вероятности случайных значений параметров регрессии меньше 1% (0,01*100%). Поэтому справедлив вывод о том, что полученные коэффициенты статистически значимы и надежны. Для а₂ делается вывод о случайной природе его значения, поскольку а=0,175*100%=17,5%>1%. Это позволяет рассматривать х₂ как неинформативный фактор. Его можно удалить из уравнения для улучшения модели.

Свободный член a₀ оценивает агрегированное влияние прочих (кроме учтенных в модели х₁и х₂) факторов на результат у. Коэффициенты а₁ и а₂ указывают на то, что с увеличением х₁и х₂на единицу их значений у увеличивается, соответственно, на 0,9459 тыс.руб. и на 0,0856 тыс.руб. Сравнивать эти значения не следует, так как они зависят от единиц измерения каждого признака и потому несопоставимы между собой. Для сравнения можно воспользоваться сравнимыми относительными показателями - β-коэффициентами (графаBETA, рис. 18).

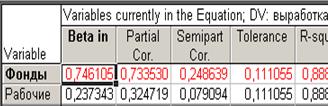
3. Оценить тесноту парных зависимостей включенных в модель факторов можно через матрицу парных коэффициентов корреляции, а тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии можно через матрицу линейных коэффициентов частной корреляции. Для построения этих матриц в модуле МНОЖЕСТВЕННАЯ РЕГРЕССИЯ (рис.17) на вкладке Advanced выбрать команду Partial correlations (для построения матрицы линейных коэффициентов частной корреляции) (рис.19Б), затем на вкладке Residuals/assuptions/prediction следует последовательно выбрать команды Descriptive statistics -> Correlations(для построения матрицы парных коэффициентов корреляции) (рис.19А).

А). Б).

Проанализируем полученный результат (Рис.19А). Значения парных коэффициентов корреляции говорят о тесной связи выработки продукции на 1 работника (у) как с коэффициентом обновления основных фондов (x₁): 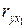= 0,97, так и с долей рабочих высокой квалификации в общей численности рабочих (х₂): = 0,94. При этом следует учитывать тесную межфакторную связь x₁ с х₂ ( = 0,94) примерно равную связи у с х₂. Поэтому для улучшения модели фактор х₂ можно исключить как недостаточно статистически надежный.

Проанализируем полученный результат (Рис.19Б). Коэффициенты частной корреляции дают более точную характеристику тесноты зависимости двух признаков, чем коэффициенты парной корреляции, так как "очищают" парную зависимость от взаимодействия данной пары признаков с другими признаками, представленными в модели. Наиболее тесно показатель выработки продукции на 1 работника (у) связана с коэффициент обновления основных фондов (x₁): = 0,73 по сравнению со связью у с долей рабочих высокой квалификации в общей численности рабочих (х₂): 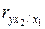= 0,32. Этот факт также говорит в пользу исключения фактора х₂ из модели.

4. Коэффициенты линейной множественной корреляции (детерминации) представлены на рис.17. Коэффициент множественной корреляции =0,973 свидетельствует о тесной связи факторных признаков с результативным.

Нескорректированный коэффициент множественной детерминации 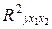= 0,947 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Он указывает на высокую степень обусловленности вариации результата вариацией факторных признаков. Скорректированный (adjusted) коэффициент множественной детерминации 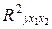= 0,941 оценивает тесноту связи с учетом степеней свободы (17), что позволяет его использовать для оценки тесноты связи в моделях с разным числом факторов.Значения коэффициентов множественной детерминации позволяют сделать вывод о высокой (более 90%) детерминированности результативного признака у в модели факторными признаками x₁ и х₂.

5. Оценим статистическую надежность полученного уравнения множественной регрессии с помощью общего F-критерия, который проверяет нулевую гипотезу о статистической незначимости параметров построенного регрессионного уравнения и показателя тесноты связи (Н₀: а₀= a₁=a₂=0, =0). Фактическое значение F-критерия Фишера: Fp=151,7 (см. рис.17). Сравним его с табличным значением F-критерия, определяемым с использованием таблицы приложения 2 по заданным уровню значимости (α= 0,05) и числу степеней свободы (17). Fт= 3,59. Поскольку Fp > F_T, то гипотеза Н₀ отвергается. Так как вероятность случайного значения Fp значительно меньше 5 % (р<0,000001, см.рис.17), то с вероятностью более чем 95 % принимается альтернативная гипотеза. Таким образом, признается статистическая значимость регрессионного уравнения, его параметров и показателя тесноты связи .

⇐ Предыдущая 7 8 9 101112 13 14 15 16 Следующая ⇒