 |
|
Вычисление погрешностей прямых измерений
Представим, что мы на опыте измерили какую-либо величину и получили всего «m» результатов отдельных измерений: N1, N2, N3…Nn –всего «n» измерений.
По сказанному выше – среднее арифметическое будет наиболее близким к истинному значению измеряемой величины:
Будем называть величину N средним арифметическим или, с некоторым приближением, истинным значением искомой величины.
Найдем разницу между отдельным каждым измерением и истинным значением измеряемой величины, т.е.
N - N1 = ±∆N1
N - N2 = ±∆N2
……………
N - Nn = ±∆Nn.
Берем знаки ±, т.к.Ni могут быть как больше, так и меньше N.
Разность между истинным значением измеряемой величины и отдельным измерением дает нам абсолютную погрешность отдельного измерения.
Среднее арифметическое из численных значений отдельных ошибок называется средней абсолютной ошибкой измерений: (абсолютные ошибки берутся по абсолютной величине)
.
Зная абсолютные погрешности отдельных измерений, можно найти относительные ошибки отдельных измерений, которые представляют собой отношение следующих величин:
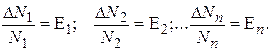
Относительные погрешности выражаются обычно в %, в то время как абсолютные – в единицах измерения искомой величины.
Отношение средней абсолютной ошибки ∆N к среднему арифметическому N называется средней относительной ошибкой измерения: 
Например: 1. Измерение времени:
| t1 = 20,0 с t2 = 19,7 с t3 = 20,1 с t4 = 19,8 с | ∆t1 = -0,1 с ∆t2 = +0,2 с ∆t3 = -0,2 с ∆t4 = +0,1 с |
| t=79,6:4=19,9 с | ∆t =0,6:4=0,15 с≈0,2 с |
Е =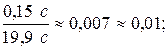 
или в процентах Е=1 %.
Искомый результат записывается: t = (19,9±0,2) с.
2. Измерение толщины пластинки:
| d1 = 2,24 мм d2 = 2,28 мм d3 = 2,20 мм | ∆d1 = 0,00 мм ∆d2 = -0,04 мм ∆d3 = +0,04 мм |
| d = 6,78:3 = 2,24 мм | ∆d = 0,08:3 мм ≈ 0,026 ≈ 0,03 мм |
, d = (2,24±0,03) мм.
Отсюда видно, что абсолютная погрешность показывает, в каких пределах находится измеряемая величина.
По абсолютной погрешности можно судить и о точности измерения однородных величин одного порядка.
Например,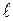 
1 = 25 см; 
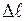1 = 0,1 см и
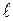2 = 50 см; 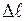2 = 0,01 см,
второе измерение сделано с точностью в 10 раз большей, чем первое.
Относительная же погрешность позволяет судить о степени точности измерения величин разных порядков как однородных, так и разнородных.
Поясним это примером: были измерены две физические величины – толщина пластинки d и скорость света c. С учетом абсолютных ошибок измерения эти величины запишутся:
d ± ∆d = (2,25 ± 0,01) мм, с ± ∆с = (300000 ± 100) км/с.
На первый взгляд (по абсолютным ошибкам измерения) кажется, что толщина пластинки измерена точнее скорости света.
Но! Значение ∆d и ∆с не позволяет судить о степени точности этих измерений. Найдем относительные погрешности:
откуда следует, что второе измерение было произведено с точностью, примерно в 10 раз большей, чем первое, что с первого взгляда было неочевидно. В том случае, когда данная физическая величина определялась много раз – теоретически число измерений равно ∞ - степень точности результата измерений можно оценить более строго, воспользовавшись формулой, которую дает теория вероятностей. Это так называемая средняя квадратичная абсолютная погрешность: 
Здесь n – число измерений, а ∑(∆Ni)2 есть сумма квадратов абсолютных ошибок отдельных измерений.