 |
|
Погрешности косвенных измерений
В большинстве случаев для получения результата надо произвести ряд прямых измерений других величин, связанных между собой определенными формулами. Зная погрешности, допущенные при измерениях этих величин, входящих в формулу для определения искомого результата, необходимо определить и погрешность самого результата. Для нахождения абсолютных и относительных погрешностей косвенных измерений удобно пользоваться следующими правилами:
1) средние абсолютные ошибки можно находить по правилам дифференцирования, заменив значок дифференцирования (d) значком ошибки (Δ). Знаки (+ или -) при этом надо выбирать так, чтобы абсолютная ошибка была max.
2) Относительную погрешность результата можно найти следующим образом: логарифмируем исходное выражение, а затем его дифференцируем, заменяя в конечном итоге значки d на значок Δ. Знаки + и – опять – таки выбираем таким образом, чтобы абсолютная величина относительной ошибки была бы максимальной.
Проиллюстрируем нахождение ΔN и Е косвенных измерений.
1. Измеряемая величина находится по формуле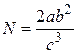 
. Величины а, b и c находятся прямыми измерениями и для них рассчитываются Δа, Δb, Δc. Необходимо найти абсолютную и относительную ошибки величины N:
Найдем ΔN:
для этого вначале продифференцируем все выражение для N:
затем значки дифференцирования заменяем наΔ и получаем абсолютную ошибку ΔN:
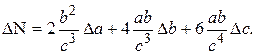
Теперь найдем Е, исходя из значения ΔN.
Из этого примера видно, что здесь проще было бы найти относительную ошибку, а затем абсолютную. Скажем сразу, что во всех тех случаях, когда искомая величина есть произведение и дробь величин, измеренных непосредственно на опыте, удобнее и легче находить в первую очередь относительную погрешность, а затем абсолютную. В самом деле:
lnN=ln2+lna+2lnb-3lnc, после дифференцирования, замены значков дифференцирования наΔ и изменения знаков так, чтобы ошибка была максимальная получаем 
.
А теперь, если нужно, можно найти и ΔN, зная, что ΔN=Е ∙N.
1.3. ИЗУЧЕНИЕ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Нониусы
Часто при измерении длины какого-либо тела длина его не укладывается в целое число делений масштаба. Для того чтобы можно было поручиться при линейных измерениях и за десятые доли масштаба (а иногда и за сотые), пользуются нониусом.
Нониус – это дополнительная шкала к основному масштабу (линейному или круговому), позволяющая повысит точность измерения с данным масштабом в 10, 20 и более число раз.
Нониусы бывают линейные и круговые, прямые и обратные, нерастянутые и растянутые.
Линейный нониус представляет собой небольшую линейку (шкалу), скользящую вдоль большей масштабной линейки (рис.2). Как видно из рис.1, 10 делений нониуса соответствуют 9 делениям основного масштаба. В случае прямого нерастянутого нониуса, который мы рассматриваем, одно деление нониуса короче одного деления масштаба на величину Δ, которая называется точностью нониуса. Точность нониуса Δ является разностью длин делений основного масштаба и нониуса и легко может быть определена, если мы знаем число делений нониуса n и длину наименьшего деления масштаба αm
.
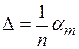Длина отрезка, измеряемая при помощи нониуса, будет равна числу целых делений масштаба до нуля нониуса плюс точность нониуса, умноженная на номер его деления, совпадающего с некоторым делением масштаба. На рис.3 длина тела равна 13 – ти целым и 3-м десятых, так как совпадает с делениями масштаба 3 – е деление нониуса.
Погрешность, которая может возникнуть при таком методе отсчета, будет обуславливаться неточным совпадение деления нониуса с одним из делений масштаба, и величина ее не будет превышать, очевидно, 
. Таким образом, можно сказать, что погрешность нониуса равна половине его точности.
Чтобы легче было заметить, какое деление нониуса совпадает с каким- либо делением основной шкалы, на практике делают нониусы растянутыми. Прямой растянутый нониус получится, если длина одного деления нониуса будет короче не одного наименьшего деления масштаба (как мы полагали до сих пор), а двух, трех и т.д. наименьших делений его.
Точность нониуса в этом случае определяется по той же формуле.
Круговой нониус в принципе ничем не отличается от линейного. Он представляет собой небольшую дуговую линейку, скользящую вдоль круга лимба, разделенного на градусы или на доли градуса (рис. 4). Точность кругового нониуса обычно выражается в минутах. Часто круговые нониусы в приборах, в которых необходимо отсчитать углы в обоих направлениях (по часовой стрелке или против нее), состоят из двух совершенно одинаковых шкал, расположенных по обе стороны от нуля
Очень часто в круговых нониусах αм=0,5о=30 минут , а n равно 15 или 30, в таком случае точность нониуса, соответственно равна двум минутам или одной минуте.
В лабораторной практике для измерения длин, площадей и объемов наиболее распространенными приборами являются штангенциркуль и микрометр.
Штангенциркуль
Штангенциркуль (рис.5) служит для линейных измерений, не требующих высокой точности.
Отсчетным приспособлением у всех конструкций штангенциркулей служит основная масштабная шкала штанги 1, цена деления которой 1 мм, и линейный нониус на подвижной рамке 2. Он представляет собой небольшую линейку, скользящую вдоль основного масштаба. На этой линейке нанесена маленькая шкала, состоящая из m делений.
При нулевом показании инструмента нуль нониуса совпадает с нулевым штрихом основной шкалы. При измерении подвижная рамка с нониусом смещается и предмет зажимается губками 3 штангенциркуля. Так как цена деления нониуса не равна цене деления масштаба, то обязательно найдется на нем такое деление, которое будет ближе всего подходить к какому-то делению масштаба.
Правило отсчета можно сформулировать следующим образом: длина предмета, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба. В лабораторной практике обычно используются штангенциркули с точностью 0,1 и 0,05 мм, которая указывается на приборе.
Для измерения внутренних размеров тел служат обычно верхние заостренные ножки 4. Если же штангенциркуль не имеет верхних ножек, то измерение внутренних размеров производится теми же ножками, которые служат для обмера наружных размеров тела; в этом случае необходимо учитывать толщину ножек штангенциркуля, которая указывается на самом инструмента. Некоторые штангенциркули снабжаются линейкой 5, служащей для измерения глубин.
В лабораторной практике широко используются также круговые нониусы в различных приборах для измерения углов.
Микрометр
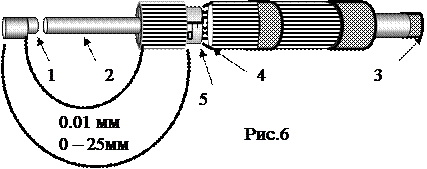Микрометр (рис.6) служит для измерений диаметров проволок, небольших толщин пластинок и т.п. Он имеет вид тисков и при измерении предмет зажимается между неподвижным стержнем 1 и подвижным торцом микрометрического винта 2. Микровинт вращают, держась за трещетку 3. На стержне микровинта укреплен барабан 4, с нанесенной на нем шкалой, имеющей 50 делений. Отсчет ведется по горизонтальной шкале 5 и по шкале барабана. Ход винта (поступательное перемещение барабана и стержня 2 при совершении одного оборота винта) равен 0,5 мм. Это означает, что цена деления барабана 0,01 мм. Следует обратить внимание, что выше основной миллиметровой шкалы имеется дополнительная линейная шкала, смещенная относительно основной на 0,5 мм.
Прежде чем пользоваться микрометром, необходимо убедиться, что микрометр исправлен – нули его шкал совпадают. Измеряемый предмет помещают между стержнем 1 и винтом 2. Затем, вращая винт за головку 3, доводят его до соприкосновения с предметом. Момент зажатия фиксируется треском. После этого треска дальнейшее вращение головки 3 бесполезно, а барабана 4 недопустимо. Отсчет производят по шкалам: миллиметры по основной линейной шкале, доли миллиметра по шкале на барабане. При отсчете необходимо учитывать, появилась ли половинка деления верхней шкалы после последнего перед краем барабана деления нижней основной шкалы или нет. На рис.7 крупным планом показаны шкалы микрометра. Как видно из рис.7 (слева), когда край барабана перешел нижнюю риску, соответствующую 6,00 мм, а риска верхней шкалы не видна, то длина измеряемого предмета равна 6,15 мм. Когда же край барабана перешел верхнюю риску (рис.7, справа), соответствующую 6,50 мм, то длина измеряемого предмета равна 6,65 мм. Нетрудно понять, что цена деления барабана, равная 0,01 мм, и является точностью прибора, которая указывается на микрометре.