Главная | Обратная связь

ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Приборы и принадлежности: прибор для наблюдения упругих (крутильных) колебаний, секундомер.

Описание прибора

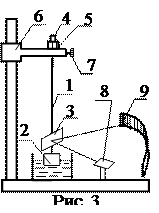
Прибор для наблюдения затухающих колебаний (рис. 3) состоит из металлической проволоки 1, верхний конец которой закреплен. На ее нижнем конце подвешен груз 2, центр тяжести которого расположен на продолжении оси проволоки; выше груза на его оси вращения закреплено зеркальце 3. Если груз повернуть на некоторый угол около вертикальной оси, то проволока закручивается и в ней появляются упругие силы. Вследствие этого система, предоставленная сама себе, начинает совершать упругие (крутильные) колебания около вертикальной оси. Таким образом, для нашего случая уравнение движения следует записать в виде: , где J – момент инерции груза относительно оси вращения; j - угол поворота, - угловое ускорение груза и M – результирующий момент действия сил. Выразив результирующий момент сил через действующие силы, а угол поворота j через смещение х – указателя (j = x/ℓ , где ℓ – длина указателя, т.е. расстояние от нити до шкалы), мы получим дифференциальное уравнение, аналогичное 4. Поэтому все дальнейшие рассуждения, приведенные в разделе «краткая теория», справедливы для данного случая.

Для того, чтобы можно было груз приводить в крутильные колебания, не сообщая ему одновременно маятникообразных колебаний, верхний конец нити прикреплен к горизонтальной шайбе 4, которая может вращаться межу упорами 5. Шайба 5 может поворачиваться во втулке кронштейна 6 и фиксироваться винтом 7, напротив груза 2 размещены осветитель 8 и горизонтальная шкала 9.

Выполнение работы

Включить осветитель. Лучи, выходящие из осветителя, попадают на зеркальце и, отражаясь от него, попадают на шкалу. Немного отвернув винт 7 и медленно вращая шайбу 5, установить зайчик на нулевую отметку шкалы и завинтить винт 7. При этом необходимо следить, чтобы шайба 4 своим выступом была прижата к одному из упоров шайбы 5.Чтобы придать грузу крутильные колебания, необходимо повернуть шайбу 4 на некоторый угол и вернуть ее в первоначальное положение.

Измеряя с помощью секундомера не менее трех раз продолжительность t 10 - 15 полных колебаний n, определить период колебаний Т по формуле Т = t/n. Данные занести в табл. 1

N п/п	n	t, с	T, с	DТ, с
Ср

Примечание. Если после прекращения колебаний окажется, что зайчик несколько отошел от нулевой отметки, его новое положение принимается за нулевое и отсчеты ведутся с соответствующей поправкой.

2. Сообщить системе крутильные колебания и измерить ряд ( не менее 10) последовательных амплитуд по ту и другую сторону от нулевой отметки прибора. По формуле (8) вычислить ряд значений декремента затухания D и данные занести в таблицу.

№ п|п	Отсчет влево	Отсчет вправо
A,см	D	DD	A,см	D	DD
….
Ср

Среднее значение декремента затухания D_ср, вычисляются по формуле .

По полученному значению D_ср определить среднее значение декремента затухания системы q_ср=lnD_ср.

По формуле (9) определить среднее значение коэффициента d_ср. Значение величины Т_ср берется из предыдущего упражнения. По имеющимся экспериментальным данным оценить относительную погрешность определения логарифмического декремента затухания q. и коэффициента затухания d.

РАБОТА № 3-2

ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОГО ДЕКРЕМЕНТА ЗАТУХАНИЯ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Приборы и принадлежности: математический маятник с электронным блоком управления.

Описание установки

Общий вид установки представлен на рисунке. Основание прибора 1 оснащено регулируемыми ножками 2, которые позволяют провести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 5 с фотоэлектрическим датчиком и шкалой 6 . На этом же кронштейне установлена ванночка с жидкостью 7, в которой происходят затухающие колебания математического маятника 8. Длину математического маятника можно регулировать при помощи воротка 9 и фиксировать винтом 10. Когда колеблющийся маятник пересекает световой луч, падающий на фоторезистор , то в цепи фототранзистора генерируются электрические импульсы. Специальная электронная схема считает число импульсов и выдает на световой индикатор 11 информацию о числе полных колебаний маятника. Одновременно электронный секундомер ведет отсчет времени и результат фиксируется на световом индикаторе 12. Зная число колебаний маятника и время, за которое они совершаются, можно определить период колебаний маятника.

Выполнение работы

Проверьте, заземлен ли прибор. Ослабив винт 10, воротком 9 установите необходимую длину маятника так, чтобы при колебаниях маятника его поводок все время находился в жидкости. Затяните винт 10. Ножками 2 выровняйте прибор, следя за тем, чтобы во время колебаний шарик не касался стенок ванночки.

Включите сетевой шнур в сеть 220В. Нажмите кнопку «СЕТЬ». При этом должна загореться лампочка фотоэлектрического датчика, а все индикаторы показывать цифру нуль. Прибор готов к работе.

Отклонив маятник на 7-8º, определите период Т его колебаний. Для этого, когда маятник начнет совершать гармонические колебания, нажмите на кнопку «СБРОС» и после 10-15 полных колебаний нажмите на кнопку «СТОП». На световых индикаторах будут зафиксированы число полных колебаний n и их продолжительность t . По формуле T=t/n определите период колебаний математического маятника. Это упражнение проделайте не менее трех раз и данные занесите в таблицу 1.

Отклонив маятник примерно на тот же угол, что и в предыдущем упражнении, измерьте ряд (не менее десяти) последовательных амплитуд по ту и другую сторону от нулевой отметки шкалы прибора. По формуле (8) вычислите ряд значений декремента затухания D и данные занесите в таблицу 2.

N n/n	Отсчет влево А, град D ΔD	Отсчет вправо А, град D ΔD
2…. ….
Cp	ХХХХ	ХХХХ

Среднее значение декремента затухания Dср по отсчетам амплитуд влево и вправо вычисляется по формуле

D_cp = (D_{cp влево} + D_{cp вправо} )/ 2

По полученному значению Dср определите среднее значение логарифмического декремента затухания системы Qср = lnDср

По формуле (9) определите среднее значение коэффициента затухания βср. Значение величины Тср берется из предыдущего упражнения.

По имеющимся экспериментальным данным оцените относительную погрешность определения логарифмического декремента затухания и коэффициента затухания.

Контрольные вопросы.

1. Какое колебание называется гармоническим?

2. Запишите уравнение движения незатухающих гармонических колебаний и его решение.

3. Запишите и объясните уравнение движения затухающих колебаний.

4. Являются ли затухающие колебания периодической функцией?

5. Каков физический смысл коэффициента затухания и логарифмического декремента затухания?

6. От чего зависит коэффициент затухания, декремент затухания?

7. Изменяется ли период колебаний при наличии сил сопротивления?

РАБОТА № 4