 |
|
Представление регулярных функций интегралами
Изучаемые вопросы: Интеграл от ФКП. Свойства интеграла. Теорема Коши. Интеграл с переменным верхним пределом. Основная формула интегрального исчисления.
2.4.1. Интеграл от ФКП
Пусть на кривой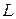 
плоскости 
задана ФКП 
(рис.1). Разобьём её на 
частей точками 
и составим интегральную сумму
, (1)
где 
. Будем бесконечно увеличивать дробление кривой 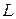так, чтобы 
. Тогда, если 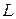– кусочно-гладкая и непрерывная, то существует конечный предел суммы 
, не зависящий ни от способа дробления, ни от выбора точки 
, и он называется интегралом от 
вдоль кривой :
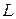. (2)
Интеграл от ФКП можно выразить через вещественные криволинейные интегралы. Пусть, как обычно,
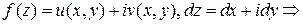
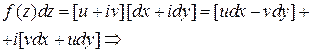
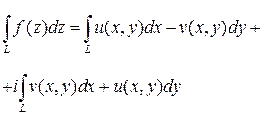
О свойствах интеграла Вы прочитаете в Учебном пособии.
2.4.2. Теорема Коши
Пусть регулярна в односвязной ограниченной области 
, тогда интеграл вдоль любой замкнутой кривой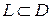 
равен нулю. Т.е.
. (1)
Примем эту теорему без доказательства, и обобщим её на многосвязные области. Но сначала отметим, что условия Коши-Римана достаточны для того, чтобы . И обратно, если непрерывна в односвязной области и , то удовлетворяет условиям Коши-Римана в этой области.
Отсюда следует второе определение регулярной функции: однозначная и непрерывная функция называется регулярной, если .
Рассмотрим двусвязную область, как на рисунке.
Проведём в области 
разрез 
и рассмотрим контур 
, начиная от точки разреза на внешней границе. Обойдём этот контур в положительном направлении, т.е. так, чтобы область оставалась слева (жирные стрелки). Тонкие стрелки означают путь по внутренней границе в отрицательном направлении, но область всё равно остаётся слева, тогда интеграл по замкнутому контуру будет равен 
по внешнему контуру равен 
по всем внутренним контурам. ( В
|
. (2)
2.4.3.
|
Пусть функция регулярна в области 
. Рассмотрим функцию 
– интеграл с переменным верхним пределом от функции . Можно доказать, что существует производная этого интеграла, причём 
. Т.е. 
, как и в вещественном анализе, является первообразной функцией для . И, также,
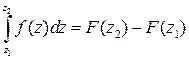. (3)
2.4.4. Интегральная формула Коши
1) Вычислим 
при целом , считая, что контур 
не проходит через точку 
. При 
, очевидно, 
. И этот интеграл будет однозначной регулярной функцией везде, при 
, или везде, кроме 
.
Пусть теперь 
. Тогда , считая что контур не проходит через точку получим интеграл 
. Если точка лежит вне контура , то, по теореме Коши, этот интеграл по любому замкнутому контуру будет равен нулю: 
.
Теперь пусть точка находится внутри контура . Тогда в точке подынтегральная функция не определена, и, значит, не регулярна. Окружим эту точку окружностью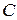 
радиуса 
(см. рисунок), тогда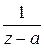 
регулярна в кольце 
.
|
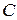
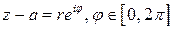– аргумент числа 
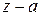. Но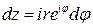 
, тогда
и не зависит от радиуса . Итак,
(4)
2) Формула Коши. Пусть регулярна в области и – контур и точка 
. Составим функцию 
. Она регулярна везде в области , кроме точки . Окружим эту точку кругом радиуса 
(см. рисунок).
В серой области эта функция регулярна везде, тогда по теореме Коши
при обходе по 
в положительном направлении. Но 
, тогда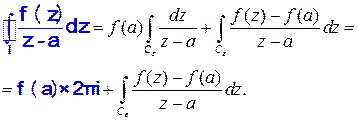 
Члены, выделенные жирным шрифтом не зависят от , а последний член можно оценить, как
поскольку 
, а при 
. Следовательно, 
. И, заменяя на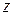 
, получаем:
. (5)
Далее, точка 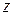лежит в области , точка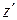 
– на линии , т.е. 
. Значит, подынтегральная функция в (5) непрерывна, и её можно дифференцировать по 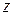под интегралом сколько угодно раз. Тогда
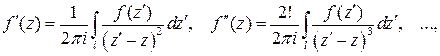
. (6)
Итак, интегральная формула Коши (5) выражает значение регулярной функции во внутренней точке области через значение этой же функции на границе области. Оказывается также, что регулярная функция имеет производные любого порядка, которые, разумеется, также являются регулярными функциями. Их можно найти по формуле (6).
Формула Коши играет важную роль в ТФКП, являясь основой для решения граничных задач.
Вопросы для самопроверки по теме 2.4
1. Что называется интегралом от вдоль кривой ?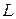
2. Как интеграл от ФКП выражается через вещественные криволинейные интегралы?
3. Сформулируйте теорему Коши для многосвязной области.
4. Дайте два определения регулярной функции.
5. Напишите основную формулу интегрального исчисления. Есть ли различия в ней для вещественного и комплексного переменного.
6. Чему равен ?
7. Напишите интегральную формулу Коши.
2.5. Представление регулярных функций рядами
Изучаемые вопросы: Функциональные ряды. Равномерная сходимость. Признак Вейерштрасса о равномерной сходимости. Степенные ряды. Теорема Абеля. Ряд Тэйлора. Разложение элементарных функций в степенные ряды. Ряд Лорана. Изолированные особые точки. Разложение в ряд Лорана в окрестности бесконечно удалённой точки.
2.5.1. Функциональные ряды
Пусть в области определены ФКП 
. Выражение
(1)
называется функциональным рядом. Ряд называется сходящимся в точке 
, если существует конечный предел частичной суммы ряда
, (2)
где 
, а сам предел 
называется суммой ряда.
Это означает, что 
такое число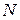 
, что для всех номеров 
. (3)
Номер 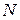зависит, в общем, от и 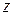, но если (3) выполняется, начиная с , независимо от положения точки 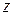в области , то ряд (1) называется равномерно сходящимся в этой области.
Существует простой признак равномерной сходимости: если ряд (1) мажорируется (или усиливается) в области сходящимся положительным числовым рядом
, (4)
т.е. для всех и 
, то ряд (1) сходится равномерно в .
При рассмотрении функциональных рядов возникают два основных вопроса: а) какова область сходимости, и б) какими свойствами обладает в этой области сумма ряда. Для решения вопроса а) используются признаки сходимости (Даламбера, абсолютной сходимости, и т.д.), а для решения вопроса б) – следующие теоремы:
Теорема 1. Если члены функционального ряда (1) непрерывны в и ряд сходится равномерно, то сумма ряда – функция, непрерывная в .
Теорема 2. Если члены функционального ряда (1) непрерывны в и ряд сходится равномерно, то сумму ряда можно интегрировать почленно вдоль любой кривой 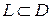, т.е.
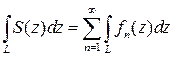. (5)
Теорема 3. (Вейерштрасса). Если члены ряда (1) являются регулярными функциями в области и он сходится равномерно в любой замкнутой области 
к сумме , то эта сумма также регулярна в , и её производные можно получить почленным дифференцированием ряда (1):
. (6)
Ряд, стоящий справа в (6) равномерно сходится в области 
.
2.5.2. Ряд Тэйлора
Степенным рядом с центром в точке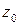 
называется ряд
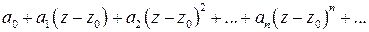. (7)
Числа 
– коэффициенты ряда (7).
Теорема Абеля. Если степенной ряд (7) сходится в точке 
, то он сходится абсолютно в круге радиуса 
с центром в точке 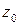, причём, в любом замкнутом круге меньшего радиуса с тем же центром его сходимость равномерна. Если же он расходится в точке , то он расходится во внешности круга радиуса с центром в 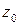. (см. рисунок).
На основании теоремы Абеля для любого степенного ряда доказывается существование радиуса сходимости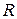 
.
Возможны три случая:
1) если 
, то ряд (7) сходится только в центре, т.е. в точке 
;
2) если 
, то ряд (7) сходится при любом ;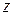
3) если 
, то он сходится в круге 
и расходится вне его. Круг
(8)
называется кругом сходимости.
Во многих случаях радиус сходимости можно найти по признаку Даламбера:
Если существует предел 
, то 
. (9)
Члены степенного ряда (7) суть регулярные функции. По теореме Абеля, внутри круга сходимости этот ряд сходится равномерно, значит, по теореме 1, сумма его регулярна внутри круга сходимости. Справедливо и обратное утверждение. Тогда можно доказать следующую теорему.
Теорема. Пусть регулярна в круге радиуса 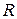с центром в 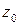. Тогда внутри этого круга её можно представить степенным рядом
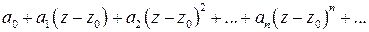= . (10)
При этом коэффициенты ряда выражаются формулой Тэйлора
. (11)
Подставив (11) в (10), получим разложение в ряд Тэйлора:
. (12)
Т.о., любая , регулярная внутри круга , представима в точках этого круга в виде суммы степенного ряда и разложение это единственно.
Функция, представимая в круге степенным рядом, называется аналитической. Для ФКП аналитичность равносильна регулярности.
Примеры вычисления ряда Тэйлора для некоторых элементарных функций Вы найдёте в Учебном пособии.
2.5.3. Ряд Лорана (РЛ)
Естественным обобщением степенного ряда является ряд Лорана. Это выражение вида
, (13)
т.е. этот ряд содержит отрицательные и неотрицательные степени 
и есть обобщение формулы (7). Части его называются соответственно главной и регулярной, или правильной. Коротко его можно записать в виде 
.
Ряд Лорана считается сходящимся, если одновременно сходятся его главная и регулярная части. Регулярная его часть – это обычный степенной ряд, и пусть его радиус сходимости 
, т.е. она сходится в круге
. (14)
В главной части сделаем замену 
, тогда получим степенной ряд
(15)
и пусть он сходится в круге 
. Сделаем обратную замену, найдём, что главная часть РЛ сходится во внешности круга радиуса с центром в :
, (16)
и если 
, то область сходимости РЛ (13) – это кольцо (см. рисунок).
. (17)
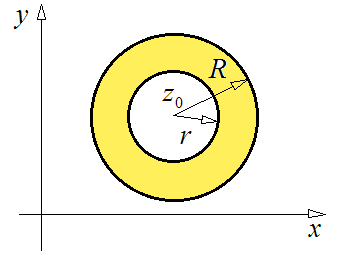
Т.е. если РЛ сходится, то его область сходимости – концентрическое круговое кольцо.
Сумма РЛ есть регулярная функция внутри кольца сходимости.
Справедливо и обратное: функция регулярная в кольце может быть разложена в РЛ.
Частным случаем является 
: кольцо – это круг с исключённым центром 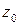. Точка 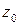в этом случае является особой, в ней не определена и имеет разрыв. Оказывается, можно установить соответствие между структурой РЛ и типом особенности функции в особой точке.
2.5.4. Изолированные особые точки ФКП
Точка 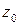называется изолированной особой точкой функции , если регулярна в некотором круге 
с исключённым центром и нерегулярна в самой точке .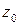
Рассмотрим виды изолированных точек:
а) 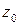называется устранимой особой точкой (ОТ) функции , если существует конечный предел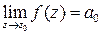 
. Для того, чтобы 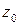была устранимой ОТ, необходимо и достаточно, чтобы РЛ в окрестности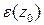 
не содержал отрицательных степеней, т.е. имел бы вид
РЛ 
.
Пример. □ 
имеет устранимую ОТ в 
. В самом деле, 
, а предел 
.■
б) особая точка 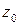называется полюсом функции , если 
.
Для того, чтобы точка 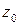была полюсом , необходимо и достаточно, чтобы главная часть РЛ в 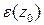содержала конечное число членов:
РЛ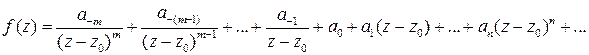 
( 
). (18)
Пусть имеет место (18). Умножим обе части его на 
:
. (19)
Здесь в знаменателе стоит степенной ряд – регулярная функция с коэффициентом , следовательно, дробь есть также некая регулярная функция 
, тогда
– регулярна в точке 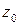и имеет в ней корень кратности 
за счёт первого множителя. Поэтому порядком полюса 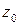функции называется кратность корня 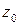функции 
, и он равен максимальной степени разности 
в главной части ряда Лорана.
в) точка 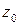называется существенно особой точкой функции , если 
не существует.
Для того, чтобы точка 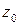была существенно особой, необходимо и достаточно, чтобы РЛ в окрестности 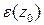содержал бесконечное число членов с отрицательными степенями.
2.5.5. Разложение в РЛ в окрестности бесконечно удалённой точки
Ранее (п.2.1), указывалось, что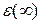 
называется внешность круга с центром в начале координат, т.е. она представляет собой кольцо с бесконечным внешним радиусом. Функция , которая регулярна в такой области, должна раскладываться в ней в РЛ по степеням 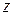. В этом случае также возможны три вида особенностей и, соответственно, три случая разложения:
а) 
, (20)
т.е., РЛ в 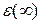не содержит положительных степеней. Тогда имеет в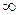 
устранимую особенность. Можно считать, что в этом случае регулярна в окрестности бесконечно удалённой точки.
б) 
, (21)
т.е. РЛ содержит конечное число членов с положительными степенями. Тогда бесконечно удалённая точка является полюсом и .
в) РЛ содержит бесконечное число членов с положительными степенями. Тогда бесконечно удалённая точка является существенно особой для .
Заметим, что при разложении в ряд Лорана в окрестности бесконечно удалённой точки смысл и название частей ряда противоположны тем, что имеют место при разложении в окрестности особой точки.
Вопросы для самопроверки по теме 2.5
1. Что называется функциональным рядом и чему равна его сумма?
2. В каком случае ряд называется равномерно сходящимся?
3. Напишите выражение для степенного ряда с центром в точке 
.
4. Пусть степенной ряд сходится в точке 
, а центр его лежит в точке . Нарисуйте круг сходимости этого ряда и укажите область расходимости.
5. Напишите формулу Тэйлора.
6. Как называются различные части ряда Лорана?
7. Можно ли функцию, регулярную в круге разложить в ряд Лорана?
8. Какие виды изолированных особых точек Вы знаете?