 |
|
Численные методы решения обыкновенных дифференциальных уравнений
Из всех вопросов темы 1.8 изучается вопрос «Численное решение задачи Коши для обыкновенного дифференциального уравнения 1-го порядка».
После изучения материала опорного конспекта и письменных лекций Вам следует решить одну из задач контрольной работы согласно "Методическим указаниям к выполнению контрольной работы".
1.8.1. Решение задачи Коши методом Эйлера
Пусть требуется найти на отрезке [a, b] решение дифференциального уравнения 1-го порядка
(1)
с начальным условием
(2)
(задача Коши). Для этого отрезок, на котором ищется решение задачи, разбивают на 
частей с шагом 
и находят значения 
в точках 
. Очевидно, что при этом 
. Значения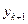 
определяют по формуле
. (3)
Погрешность вычислений на каждом шаге составляет 
, где 
.
Пример. Решить задачу Коши для обыкновенного дифференциального уравнения 1-го порядка методом Эйлера. Вычисления выполнять с четырьмя десятичными знаками на отрезке [0,2; 1,2] с шагом 0,1. Уравнение:
,
начальное условие: 
.
○ Для численного решения заданного уравнения вида (1) с начальным условием (2) нам потребуется выполнить 
шагов. На каждом шаге надо вычислить значения 
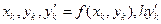и .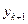
Первый шаг. (k = 0). Имеем:
; 
. Вычислим
.
Тогда 
и, следовательно, по формуле (3) 
. Делаем следующий шаг.
Второй шаг. (k=1).
.
Вычислим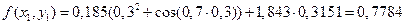 
.
Тогда 
и 
. И т.д.
Для удобства, все вычисления удобно представить в виде таблицы 1.
Таблица 1.
| 
| 
| 
| 
|
|
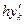
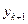
| 0,2 | 0,25 | 0,6513 | 0,0651 | 0,3151 | |
| 0,3 | 0,3151 | 0,7784 | 0,0778 | 0,3929 | |
| 0,4 | 0,3929 | 0,9316 | 0,0932 | 0,4861 | |
| 0,5 | 0,4861 | 1,1160 | 0,1116 | 0,5977 | |
| 0,6 | 0,5977 | 1,3371 | 0,1337 | 0,7314 | |
| 0,7 | 0,7314 | 1,6019 | 0,1602 | 0,8916 | |
| 0,8 | 0,8916 | 1,9184 | 0,1918 | 1,0835 | |
| 0,9 | 1,0835 | 2,2962 | 0,2296 | 1,3131 | |
| 1,0 | 1,3131 | 2,7466 | 0,2747 | 1,5878 | |
| 1,1 | 1,5878 | 3,2829 | 0,3283 | 1,9161 | |
| 1,2 | 1,9161 | 3,2912 | 0,3291 | 2,3081 |
Т.о., задача решена. ●
Естественно, процесс вычислений проще организовать в табличном процессоре Excel (Табл.2).
Таблица 2.
Решение находятся в ячейках 
(k = 0,1,…,10). Значения 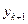из столбца F переносятся в столбец С со сдвигом на единицу (например, из F6 в С7 и т.д.). Таблица в режиме показа формул – (табл.3).
Таблица 3.
Вопросы для самопроверки по теме 1.8
1. В чём состоит задача Коши?
2. Напишите расчётную формулу метода Эйлера при решении дифференциального уравнения 1-го порядка и формулу оценки погрешности на каждом шаге.