 |
|
Функции комплексного переменного (ФКП). Условия Коши-Римана
Изучаемые вопросы: Определение ФКП. Предел и непрерывность. Производная и дифференциал. Необходимое и достаточное условие дифференцируемости. Правила дифференцирования. Регулярность. Гармонические функции.
По этой теме Вам также предстоит решить задачу контрольной работы (см. [4]).
2.2.1. Общие замечания
Все нужные определения и примеры приведены в Учебном пособии.
При изучении материала обратите внимание на схожесть понятий для ФКП и функций вещественного переменного. Различие в понятиях бесконечности на вещественной оси и бесконечно удалённой точки (БУТ) на комплексной плоскости основано на следующем.
Понятие БУТ вводится по аналогии с расширением вещественной оси, к которой добавляют две «бесконечные» точки: 
и 
. Комплексная плоскость с добавленной БУТ также называется расширенной. Геометрическую интерпретацию этого понятия дал Риман (сфера Римана).
Рассмотрим сферу произвольного радиуса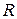 
, касающуюся комплексной плоскости 
в начале координат 
(рис.1). Пусть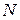 
– верхний конец вертикального диаметра (северный полюс). Любое к.ч. изображается точкой 
на комплексной плоскости. Соединим эту точку с полюсом 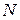, и пусть 
– точка пересечения прямой 
со сферой. Точка называется стереографической проекцией точки 
. Тогда 
. Наоборот, 
. Соответствие будет однозначным, если считать, что 
. Тогда, при 
, т.е. окрестностью БУТ следует считать множество точек расширенной комплексной плоскости: 
, т.е. внешность любого круга радиуса 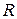с центром в начале координат .
Необходимыми и достаточными условиями дифференцируемости ФКП являются условия Коши-Римана, которые совпадают с уравнениями (1). Следует запомнить все четыре выражения для производной ФКП через частные производные её вещественной и мнимой частей:
(2)
Важным в ТФКП является понятие регулярной функции: функция однозначная и дифференцируемая в каждой точке некоторой области называется регулярной в этой области. Из этого определения следует, что для регулярной функции выполняются условия Коши-Римана.
Функция, регулярная в окрестности некоторой точки, называется регулярной в этой точке. Оказывается, что функция, регулярная в точке, имеет в этой точке производные любых порядков.
Функции, удовлетворяющие уравнению Лапласа
, (3)
называются гармоническими функциями. Уравнение (3) имеет большое значение в электродинамике, описывая потенциал постоянного электрического поля в пустоте.
Вопросы для самопроверки по теме 2.2
1. В чём заключаются условия Коши-Римана?
2. Напишите четыре уравнения для вычисления производной ФКП.
3. Что означает регулярность функции?
4. Какие функции называются гармоническими?