 |
|
Система уравнений, описывающая движение рабочего тела в обогреваемой трубе.
В установившемся режиме движение переменные параметры среды в любом поперечном сечении трубы не меняются во времени, т.е. все параметры являются только функцией продольной координаты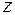 
. Все локальные производные 
, где под «у» понимаются переменные параметры.
В соответствии с этим исходная система уравнений, описывающая движение жидкости в обогреваемой трубе для установившегося режима примет вид:
1) 
- уравнение неразрывности;
2) 
- уравнение изменения количества движения;
3) 
- уравнение сохранения энергии для рабочего тела;
4) 
- уравнение сохранения энергии для металла трубы;
5, 6) замыкающие зависимости и уравнения состояния остаются без изменения.
Интегрирование системы уравнений начнём с уравнения неразрывности. . Равенство нолю производной выполняется, когда переменная 
постоянна. Как уже отмечалось ранее, произведение 
равно массовому расходу 
, который сохраняет своё значение в любом поперечном сечении трубы.
Если труба имеет постоянный диаметр, то массовая скорость 
также постоянна в любом сечении, т.е. 
где индексы «н» и «к» относятся к сечению на входе и выходе из трубы.
Из постоянства массового расхода следует, массовая скорость зависит от поперечного сечения трубы и может изменяться, если 
: 
, где 
- площадь поперечного сечения трубы с координатой .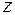
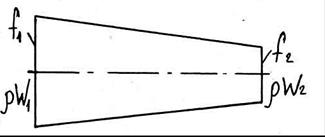
Рисунок
Зная массовый расход «D» и площадь сечения легко найти массовые скорости в этих сечениях из уравнения неразрывности:
, откуда
.
В необогреваемой трубе энтальпия не меняется вдоль трубы, поэтому в соответствии с уравнением состояния плотность среды также остаётся постоянной.
Линейная скорость 
в силу постоянства массовой скорости 
в этом случае не меняется вдоль оси.
Для обогреваемой трубы в каждом сечении трубы плотность будет разная, т.к. энтальпия потока увеличивается в направлении движения. Как видно из рисунка 5, 6. С увеличением энтальпии 
плотность 
уменьшается, что вызывает рост линейных скоростей 
, при этом , согласно уравнению неразрывности.
Проинтегрируем уравнение сохранения энергии для рабочего тела.
- это уравнение с разделяющимися переменными.
. (10)
В соответствии с уравнением неразрывности, массовая скорость в установившемся режиме для трубы поперечного сечения является постоянной величиной. Постоянны также периметр 
и внутренний диаметр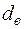 
трубы.