 |
|
Изменение энтальпии рабочего тела вдоль равномерно обогреваемой трубы.
Тогда, преобразовав уравнение (10), получим:
или 
.
Интеграл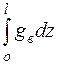 
может быть найден, если известна зависимость плотности теплового потока 
от координаты z . Наиболее просто он находится для случая, когда не меняется вдоль трубы, т.е. является постоянной величиной. Тогда, проинтегрировав уравнение (11), получим:
,
где 
- энтальпия среды на выходе и на входе в трубу и длина обогреваемой части трубы.
Произведение 
представляет внутреннюю поверхность трубы, а 
- теплоту, воспринятую рабочей средой в единицу времени. Тогда интеграл уравнения сохранения энергии для рабочего тела запишется в виде
,
где 
- приращение энтальпии рабочего тела, 
;
- массовый расход.
Представляет интерес зависимости изменения энтальпии рабочего тела вдоль оси. Её можно получить, если проинтегрировать уравнение (11) для случая, когда координата z меняется от ноля до текущего значения, т.е. нужно взять интеграл
, откуда 
(11)
Т.е. текущее значение энтальпии 
изменяется пропорционально координате z , если плотность теплового потока постоянна на всей длине трубы (рисунок 8).
Рисунок 8
На практике, как правило, плотность теплового потока имеет сложную зависимость от координаты z. Пример её для трубы экрана топки показан на рисунке 9.
Рисунок 9
Если зависимость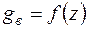 
удаётся выразить аналитически, то подставив её в подинтегральное выражение, можно взять интеграл.
В инженерных расчётах поступают проще. Длину трубы разбивают на участки, в пределах которых плотность теплового потока принимается постоянной величиной, равной
,
где «j» - номер участка;
- координаты конца и начала участка «j».
Для примера на рисунке 9 выделено 3 участка по высоте, где плотности теплового потока определены 
как средние по теореме Коши.
При таком подходе приращения энтальпии рабочего тела в трубе определится как сумма приращений энтальпии на участках:
,
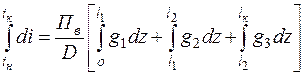, (12)
или
,
где 
- приращения энтальпии на 1, 2, 3 участках.