 |
|
Тема : Методика решения задач по теме «Физические свойства жидкостей».
Елабужский институт Казанского федерального университета.
Инженерно-технологический факультет
Кафедра общей инженерной подготовки
Гидравлика. Гидравлические машины. Гидравлические и пневматические системы.
Методические указания по решению задач. Контрольные задания.
Для студентов ОЗО.
Составил: доц. Киреев Б.Н.
Специальность : 190700. 62 (23.03.01).
Число часов согласно учебному плану:
Лекции: 6 час, семинарские -2 час, лабораторные работы-6 ч.
Форма контроля: зачёт и контрольная работа.
В разделе приведена методика решения типовых задач по темам:
Физические свойства жидкостей; 2.Основы гидростатики; 3.Основы гидродинамики; 4.Гидравлические машины: гидронасосы, гидродвигатели.
Решения снабжены рисунками и подробными пояснениями. Единицы измерения всех использованных величин приведены в системе СИ.
Тема : Методика решения задач по теме «Физические свойства жидкостей».
Цель: изучить методику решения задач по использованию таких основных свойств жидкостей, как плотность, сжимаемость, вязкость.
Задание 1. Прежде чем приступать к изучению методики решения задач на эту тему, необходимо изучить лекционный материал по данной тематике.
Задание 2. Изучить методику решения типовых задач по данной теме, используя приведенные ниже примеры
Задача 1-1. Определить избыточное давление на дне океана, глубина которого Н=5 км, приняв плотность морской воды ρ0 = 1025 кг/м3 и считая ее несжимаемой. Определить плотность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости к=2020 МПа.
Решение
Избыточное давление на глубине Н без учёта сжимаемости воды: Р = ρgH= 1025 кг/м3•9,8 м/с2•104 м = 10,04 •107 Па = 100,4 МПа. Модуль объёмной упругости k = -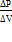 
∙ v. Сжимаемость жидкости: βр= 1/к = - (dV/V0)·(1/dp). Заменяем значения бесконечно малых изменений dV на значения конечных изменений объёма ∆V и находим значения сжимаемости: βр= 1/к = - (∆V/V0)·(1/∆p). βр= 1/к = 1/(2020 МПа) = 4,95 •10 -10 (1/Па). Конечное значение объёма V= V0·(1- βр·∆p). По определению удельного объёма υ = V/m. Следовательно, υ = υ0 ·(1- βр·∆p). Величина плотности ρ= 1/υ (величина, обратная удельному объёму) При давлении Р: ρ=ρ0/(1- βр·∆p) = 1025 кг/м3/[(1-4,95•10-10 (1/Па)•100,4•106 Па] = 1025 кг/м3/[(1-0,05]==1079 кг/м3
Ответ: значения плотности морской воды на глубине 5 км ρ =1079 кг/м3
Задача 1- 2. Трубопровод диаметром d = 100 мм и длиной L = 500 м наполнен водой при давлении 400 кПа, и температуре воды 100C. Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до 20 0C, если коэффициент объемного сжатия βр = 4,9 •10-10 (1/Па). а коэффициент температурного расширения αт = 1,8•10-4 (1/0С).
Решение.
Находим объем воды в трубе при
t= 10 0C: V0 = (πd2/4) • L = [3,14• (0,1 м)2/4] •500 м = 3,925 м3 Находим увеличение объема V при изменении температуры. Из определения коэффициента температурного расширения жидкости: αт = (∆V/ V0)/∆ t. Отсюда: ∆V = V0•αт •∆ t =3,925 м3•1,8•10-4 (1/0С) •100С = 7,065 •10-3м3 Но так как расширением и деформацией стенок трубы мы пренебрегаем, увеличение объёма жидкости должно привести к увеличению давления (чтобы объём жидкости за счёт сжатия остался неизменным. По определению коэффициента сжимаемости βр= - (∆V/V0)·(1/∆p). Отсюда находим изменение давления, соответствующее данному изменению объёма: ∆р = (∆V/V0)/ βр= (7,065 •10-3м3/3,925 м3)/4,9 •10-10 (1/Па)= 3,7 •106Па = 3700 кПа
р – р0 = 3,7 •106Па . р = 400 кПа + 3700 кПа = 4100 кПа = 4,1 МПа. Ответ: конечное давление в трубопроводе составит 4,1 МПа
Задача 1-3. Определить коэффициент динамической и кинематической вязкости воды, если шарик d=2 мм , из эбонита, плотность которого ρэ=1,2•103кг/м3 падает в воде с постоянной скоростью u = 0,33 м/с. Плотность воды ρв=103кг/м3.
Решение.
При движении шарика в жидкости с постоянной скоростью результирующая сила, равная сумме трёх сил- силы сопротивления движению Fc, силы тяжести Fт и выталкивающей силы Fвыт - равняется нулю (согласно второму закону Ньютона Fрез= m•a=0, так как ускорение равно нулю). Fрез= Fт- Fвыт-Fс = m•a=0 (1)Fc= Fт- Fвыт (2)
Рис.1.Схема сил, действующих на падающее равномерно тело в жидкости.
Сила сопротивления определяется по формуле Стокса: Fc= 6π•r•η•u = 3π• d• η • u. (3) Вес шарика определяется по формуле:Fт=mg= ρэ • V • g = ρэ • (π• d3/6) • g. (4) Выталкивающая сила равна весу вытесненной жидкости: Fвыт= ρв • V • g = ρв • (π• d3/6) • g (5).Подставляем в формулу (2) значения сил из (3), (4) и (5), получаем: 3π• d• η • u = ρэ • (π• d3/6) • g - ρв • (π• d3/6) • g (6) Из формулы (6) находим значение динамической вязкости воды: η = [(ρэ - ρв)• (π• d3/6) • g] / (3π• d • u) = [(ρэ - ρв)• d2 • g] / (18• u)η
η = [(1,2•103кг/м3- 103кг/м3) • (2• 10-3м)2•9,8 м/с2]/(18•0,33 м/с) = 1,32 •10-3 Па •с Коэффициент кинематической вязкости: χ = η / ρв = 1,32 •10-3 Па •с/103кг/м3 = 1,32 • 10-6 м2/с.
Ответ: коэффициент кинематической вязкости воды при комнатной температуре χ =1,32 • 10-6 м2/с.