 |
|
Тема : Методика решения задач по теме «Основы гидродинамики».
Цель: изучить методику решения задач по использованию таких основных понятий и законов гидродинамики жидкостей, как напор жидкости, расход, неразрывность струи, уравнение Бернулли, потери напора.
Задание 1. Прежде чем приступать к изучению методики решения задач на эту тему, необходимо изучить лекционный материал по данной тематике.
Задание 2. Изучить методику решения типовых задач по данной теме, используя приведенные ниже примеры
Задача 4-2.Разность показаний трубки Пито и пьезометрической трубки составляет 20 см. Определить расход жидкости в данном сечении трубки, если диаметр его равен 20 мм.
Трубка (справа, изогнутая) измеряет сумму пьезометрического и скоростного напоров.

Рис. к задаче 3-2.
Прямая, пьезометрическая трубка, измеряет только пьезометрический напор. Их разница и даст скоростной напор.
Решение:
Из сказанного выше следует:
Н - Hп = Hск = (u2 / 2 g);
 Расход жидкости и скорость её движения связаны соотношением
Расход жидкости и скорость её движения связаны соотношением

 Q = u · S = S·√ 2g ·Hск= S·√ 2g · (Н-Hп ) = (πd2/4) · √2g · (Н-Hп ) =
Q = u · S = S·√ 2g ·Hск= S·√ 2g · (Н-Hп ) = (πd2/4) · √2g · (Н-Hп ) =
 = [3,14· (0,02 м)2/4] · √ 2 ·9,8 · м/с2 · 0,2 м= 3,14 · 10-4 · 1,98 м3/с = 6,22·10-4 м3/с = 0,62 л/с.
= [3,14· (0,02 м)2/4] · √ 2 ·9,8 · м/с2 · 0,2 м= 3,14 · 10-4 · 1,98 м3/с = 6,22·10-4 м3/с = 0,62 л/с.
Ответ : расход жидкости равен 0,62 л/с.
Задача 4-3.Разность пьезометрических напоров в сечениях 1-1 и 2-2 равна 30 см. Определить коэффициент линейных потерь на участке между сечениями 1 и 2, если длина участка трубы L =1 м, диаметр трубы d=20 мм, а расход жидкости, протекающей по трубе Q=0,54 л/с.
Решение:
Запишем уравнение Бернулли в общем виде для потока реальной жидкости:
[ z1 +(Р1/ρg) + (α1·u1ср2/2g)]–[z2+(Р2 /ρg)+(α2·u2ср2/2g)]= h1-2
Коэффициенты Кориолиса возьмём равными 1, так как о них в условиях задачи нет сведений. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одинаковы. Их разность тоже равна нулю. С учётом сказанного уравнение Бернулли принимает вид:
(Hп1 - Hп2 ) = h1-2
Важный вывод: в горизонтальных трубах постоянного диаметра полные потери напора численно равны разности пьезометрических напоров в выбранных сечениях 1-1 и 2-2.
 Рис. к задаче 3-3.
Рис. к задаче 3-3.
Так как на данном участке трубы местные сопротивления отсутствуют, полные потери равны линейным потерям напора. Согласно формуле Дарси:
hл = λ · (L/d) · (u2 / 2 g)Следовательно, в данном случае (Hп1 - Hп2 ) = λ · (L/d) · (u2 / 2 g) .Отсюда находим коэффициент линейных потерь:
λ = (Hп1 - Hп2 ) 2 g·d / ( L·U2)
Скорость движения жидкости в трубе находим через расход жидкости:
U = Q / S ; S = πd2/4= 3,14· (0.02м)2=3,14 ·10-4 м2
Подставляем значения и находим скорость
U = Q / S= (0,54 ·10-3м3/с)/ 3,14 ·10-4м2= 1,72 м/с.
Находим коэффициент линейных потерь:
λ = (Hп1 - Hп2 ) 2 g·d / L·U2 =(0,3 м·2·9,8 м/с2·0,02 м)/1 м·(1,72 м/с)2=0,04
Ответ: коэффициент линейных потерь на участке трубы составляет 0,04.
Задача 4-4. В горизонтально расположенной трубе диаметром 6,0 см на расстоянии L = 10 м друг от друга расположены два манометра, между которыми находится кран, имеющий коэффициент местного сопротивления ε =2,7. Определить коэффициент линейных потерь на участке между сечениями 1 и 2, если разность показаний манометров рав-на 2,16 кПа, а расход жидкости в трубе составляет 2 л/с. Жидкость – вода, при 200С (плотность ρ =103 кг/м3,а динамическая вязкость η=10-3 Па  с.
с.
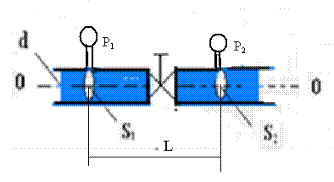 Рис. к задаче 3-4.
Рис. к задаче 3-4.
Решение:
Запишем уравнение Бернулли в общем виде для потока реальной жидкости:[  +(
+(  /2g)]- [
/2g)]- [  +(
+( 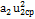 /2g)]=
/2g)]=  Коэффициенты Кариолиса определим, рассчитывая число Рейнольдса. При Re> 4000 (режим течения турбулентный) коэффициент Кориолиса равен 1, а при Re< 2300 (режим течения ламинарный) коэффициент Кориолиса равен 2. Находим число Рейнольдса:Re= ρ
Коэффициенты Кариолиса определим, рассчитывая число Рейнольдса. При Re> 4000 (режим течения турбулентный) коэффициент Кориолиса равен 1, а при Re< 2300 (режим течения ламинарный) коэффициент Кориолиса равен 2. Находим число Рейнольдса:Re= ρ  U
U  d/η. Скорость течения воды:U=
d/η. Скорость течения воды:U=  = 4
= 4  2
2  10-3(м3/с)/3,14
10-3(м3/с)/3,14  (0,06 м)2 =
(0,06 м)2 =  = 0,71 м/с
= 0,71 м/с
Re= ρ  U
U 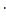 d/η = 103 кг/м3
d/η = 103 кг/м3  0,71 м/с
0,71 м/с  0,06 м/10-3 Па
0,06 м/10-3 Па  с= = 42600.Режим турбулентный, α = 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одина-ковы. Их разность тоже равна нулю. С учетом сказанного, уравнение Бернулли принимает вид: (Р1-Р2)/
с= = 42600.Режим турбулентный, α = 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одина-ковы. Их разность тоже равна нулю. С учетом сказанного, уравнение Бернулли принимает вид: (Р1-Р2)/ 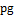 =
= 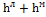 . Согласно Дарси:
. Согласно Дарси:  =λ
=λ  (L/d)
(L/d) 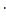 (
( 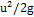 );
); 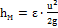 ;Следовательно, в данном случае:(Р1-Р2)/
;Следовательно, в данном случае:(Р1-Р2)/ 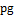 = λ
= λ  (L/d)
(L/d) 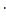 (
( 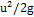 )+
)+  . Отсюда находим коэффициент линейных потерь:(Р1-Р2)= ρ
. Отсюда находим коэффициент линейных потерь:(Р1-Р2)= ρ 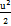 [λ
[λ  (L/d)+
(L/d)+  ]; λ
]; λ  L/d) +
L/d) +  =
=  .
.
λ  L/d) =
L/d) =  -
- 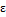 ; λ=
; λ= 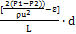 λ=
λ=  = 0,035
= 0,035
Ответ: коэффициент линейных потерь на участке трубы между сечениями 1 и 2 составляет λ = 0,035.
Задача 4-5. По трубе диаметром 5,06 см течёт вода со скоростью 1 м/с. Принимая плотность жидкости равной 1г/см3 , а динамическую вязкость 0,001 Па·с, определить число Рейнольдса, а затем коэффициент линейных потерь.
Решение:
Число Рейнольдса определяется следующим образом:Re = Red = ρ · u · d/ η ;
Re=(103кг/м3 ·1 м/с·5,06 см)/10-3Па·с= [(103·1·5,06·10-2) кг/м·с] / (10-3 н ·с/ м2) = 5,06 ·10 4
н ·с/ м2 = кг ·м · с / м2 · с2= кг/м· с; (кг/м· с)/ (кг/м· с) = 1.
Число Рейнольдса оказалось больше критического. Для нахождения коэффициента Дарси (коэффициента линейных потерь) используем формулу Блазиуса:
λ = 0,3164/ (Re0,25) = 0,3164 / (5,06 ·10 4 )0,25 = 0,3164/ 15 = 0,02.
Ответ:Re = 5,06 ·10 4 ; λ = 0,02.
Примечание: формула Блазиуса используется для нахождения коэффициента линейных потерь в случаях, когда 4000 <Re<105
Задача 4-6. Из широкого бака вытекает по трубе вода со скоростью 2,5 м/с. Определить расстояние от поверхности воды в баке до оси трубы, если полные потери напора в трубе составляют 0,6 м. Диаметр трубы одинаков по всей её длине.
Решение:
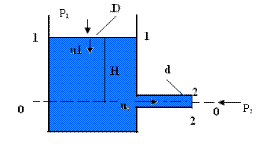
Проанализируем уравнение Бернулли для данного случая. За нулевой уровень примем линию 0-0, совпадающую с осью трубы. Первый геометрический напор по определению z1 = Н, а второй z2 = 0. Пьезометрические напоры в сечениях 1-1 и 2-2 одинаковы, так как (Р1/ ρg) = (Ратм/ ρg) ; (Р2/ ρg) = (Ратм/ ρg); и Hп1 - Hп2 = 0.
-
Рис. к задаче 4-6.
Уравнение Бернулли для данного случая принимает следующий вид:
Н =(u22/ 2g) + h1-2 ; Н = (6,25 м2/с2)/ (2·9, 8 м/с2) +0,6 м = 0,92 м.
Ответ: расстояние от уровня поверхности жидкости в баке до центра трубы равно
Н= 0,92 м.