 |
|
Закон сохранения энергии в механике
Как доказано ранее изменение кинетической энергии равно алгебраической сумме работ всех внешних и внутренних сил, действующих на систему:
∆К=Авнешн.+Авнутр. = Авнешн. + Авнутр. конс. + Авнутр. дисс., (1)
т.е. разделили внутренние силы на консервативные и диссипативные.
Работа внутренних консервативных сил равна убыли потенциальной энергии системы: Авнутр. конс. =  ∆П. (2)
∆П. (2)
Из уравнений (1) и(2) следует: ∆К = Авнешн. + Авнутр. дисс.  ∆П. Откуда следует: ∆К + ∆П = ∆(К + П) = Авнешн. + Авнутр. дисс. (3)
∆П. Откуда следует: ∆К + ∆П = ∆(К + П) = Авнешн. + Авнутр. дисс. (3)
Полной механической энергией системы называется сумма её кинетической и потенциальной энергий: Ем = К + П. (4)
Из уравнений (3) и (4) следует: ∆Ем = Е2 – Е1 = Авнешн. + Авнутр. дисс., (5)
т.е. работа есть мера изменения полной механической энергии системы.
Если механическая система изолирована, то Авнешн. = 0, тогда:
∆Ем= Авнутр.дисс.<0, тогда: ∆Ем= Е2 – Е1 < 0 и Е2< Е1, (6)
т.е. за счёт работы внутренних диссипативных сил полная механическая энергия системы уменьшается.
Если в замкнутой механической системе (Авнешн. = 0) не действуют диссипативные силы (Авнутр. дисс. = 0), тогда: ∆Ем = Е2 – Е1 = 0, т.е. Ем = сonst.
Закон сохранения полной механической энергии системы:
в инерциальной системе отсчёта полная механическая энергия замкнутой системы частиц, в которой не действуют диссипативные силы, сохраняется в процессе движения: Ем = К + П = сonst.
Как доказано в современной физике, закон сохранения энергии есть следствие симметрии пространства и времени, а именно – однородности времени [16].
Удар твёрдых тел
Удар твёрдых тел – это совокупность явлений, возникающих при становлении твёрдых тел, а также при некоторых видах взаимодействия твёрдого тела с жидкостью или газом (удар струи о тело, действие взрывной волны и т.д.).
Промежуток времени, в течение которого длиться удар, очень мал (  10-4
10-4  10-5 с), а развивающиеся на площадках контакта соударяющихся тел силы очень велики. За время удара они изменяются в широких пределах и достигают значений, при которых средние величины давления на площадках контакта равны 109
10-5 с), а развивающиеся на площадках контакта соударяющихся тел силы очень велики. За время удара они изменяются в широких пределах и достигают значений, при которых средние величины давления на площадках контакта равны 109  1010 Па. Следствиями удара являются значительные изменения за время удара скоростей точек тела, остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств их материалов и др., а при скоростях соударения, превышающих критические, - разрушение тел в месте удара.
1010 Па. Следствиями удара являются значительные изменения за время удара скоростей точек тела, остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств их материалов и др., а при скоростях соударения, превышающих критические, - разрушение тел в месте удара.
При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и в так называемую внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением их температуры.
Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов динамики. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
Основные величины, характеризующие удар твёрдых тел
При ударе кинетическая энергия соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Относительная скорость 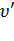 тела после удара не достигает своей прежней величины
тела после удара не достигает своей прежней величины 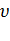 . Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.
. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.
Отношение нормальных составляющих относительных скоростей до и после удара называется коэффициентом соударения  :
:  =
=  .
.
Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Если для соударяющихся тел  = 0, то такие тела называются абсолютно неупругими, если
= 0, то такие тела называются абсолютно неупругими, если  = 1 – абсолютно упругими.
= 1 – абсолютно упругими.
На практике для всех тел 0  < 1. Однако в ряде случаев тела можно с большой точностью рассматривать либо как абсолютно упругие, либо как абсолютно неупругие.
< 1. Однако в ряде случаев тела можно с большой точностью рассматривать либо как абсолютно упругие, либо как абсолютно неупругие.
Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара.
Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центр масс.
Мы ограничимся рассмотрением центрального удара двух шаров. При центральном ударе соударение может произойти, если: 1) шары движутся навстречу друг другу (рис. 62,а) и 2) один из шаров догоняет другой (рис. 62,б).
Будем предполагать, что шары образуют замкнутую систему или что внешние силы, приложенные к шарам, уравновешивают друг друга.

Рис. 62. 1) шары движутся навстречу друг другу (а) и 2) один из шаров догоняет другой (б).
1). Абсолютно упругий удар
Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются двумя условиями — сохранением полной энергии и сохранением полного импульса системы тел.
Обозначим скорости шаров, массы которых m1 и m2, до удара:  и
и  , после удара:
, после удара:  и
и  . Так как удар центральный, то будем рассматривать модули величин. Направление движения первого тела будем считать положительным, а второго – отрицательным.
. Так как удар центральный, то будем рассматривать модули величин. Направление движения первого тела будем считать положительным, а второго – отрицательным.
Законы сохранения импульса и энергии в рассматриваемом случае:
m1 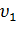 + m2
+ m2  = m1
= m1  + m2
+ m2  (1)
(1)
 +
+  =
=  +
+  . (2)
. (2)
Преобразовав уравнения в соотношениях (1) и (2), получим:
m1( 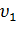 -
-  ) = m2 (
) = m2 (  -
-  ), (3)
), (3)
m1( 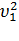 -
-  ) = m2 (
) = m2 (  -
-  ). (4)
). (4)
Из уравнения (3) следует: m1 = m2  (5)
(5)
Подставив уравнение (5) в уравнение (4) и проведя необходимые преобразования, получим: 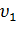 +
+  =
=  +
+  . (6)
. (6)
Произведя ряд элементарных преобразований с уравнениями (3), (4) и (6), получим:
m1( 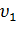 -
-  ) (
) ( 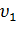 +
+  ) = m2 (
) = m2 (  -
-  ) (
) (  +
+  ),
),
m1( 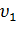 -
-  )
)  = m2 (
= m2 (  -
-  )
)  +
+  ),
),
m1 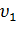 - m1
- m1  = m2
= m2  + m2
+ m2  m2
m2 
m2  + m1
+ m1  = m1
= m1 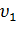 - m2
- m2 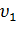 +
+  m2
m2 
 (m1 + m2) = (m1 - m2)
(m1 + m2) = (m1 - m2) 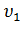 +
+  m2
m2  .
.
В итоге получаем:
 =
=  ,
,
 =
=  .
.
В случае макроскопических тел абсолютно упругий удар в чистом виде не случается. При столкновении атомных, ядерных и элементарных частиц этот случай может реализоваться в чистом виде, что связано с квантовыми закономерностями.
2). Абсолютно неупругий удар
Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергии тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся.
При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается — имеет место закон сохранения суммарной энергии различных видов – механической и внутренней. В результате абсолютно неупругого удара тела объединяются, двигаясь дальше как единое целое (рис. 63).

Рис. 63.
Рассмотрим вначале абсолютно неупругий удар. Если массы тел m1 и m2, их скорости до удара  и
и  ;
;  - общая скорость тел после удара, то, по закону сохранения импульса получаем: m1
- общая скорость тел после удара, то, по закону сохранения импульса получаем: m1  + m2
+ m2  = (m1 + m2)
= (m1 + m2) 

 =
=  . (7)
. (7)
Вследствие деформации тел при неупругом ударе происходит потеря кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту потеря равна разности кинетических энергий тел до и после удара:
∆К = (  +
+  )
) 
 .
.
Используя соотношение (1), получим: ∆К =  (
( 
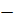
 )2 .
)2 .
Если ударяемое тело было первоначально неподвижно (  = 0), то
= 0), то  =
=  , ∆К =
, ∆К = 
 .
.
Когда m2  m1 (масса неподвижного тела очень большая), то
m1 (масса неподвижного тела очень большая), то 
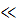
 и почти вся кинетическая энергия тела при ударе переходит в другие формы энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей масса молотка должна быть гораздо больше массы гвоздя (m1
и почти вся кинетическая энергия тела при ударе переходит в другие формы энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молотка. Наоборот, при забивании гвоздей масса молотка должна быть гораздо больше массы гвоздя (m1  m2), тогда
m2), тогда 

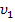 и практически вся энергия удара затрачивается на возможно большее перемещение гвоздя после удара, а не на остаточную деформацию стены.
и практически вся энергия удара затрачивается на возможно большее перемещение гвоздя после удара, а не на остаточную деформацию стены.
Примеры.
1).Каков максимальный угол  упругого рассеяния
упругого рассеяния  - частицы на дейтроне? Дейтрон – ядро одного из изотопов водорода – дейтерия, состоит из протона и нейтрона;
- частицы на дейтроне? Дейтрон – ядро одного из изотопов водорода – дейтерия, состоит из протона и нейтрона;  - частица – ядро гелия, состоит из двух протонов и двух нейтронов. Считайте, что масса дейтрона в 2 раза меньше массы
- частица – ядро гелия, состоит из двух протонов и двух нейтронов. Считайте, что масса дейтрона в 2 раза меньше массы  - частицы (рис. 64).
- частицы (рис. 64).
Решение.
Проанализируем упругое столкновение в лабораторной системе отсчёта (не прибегая к модели упругих шаров). Введём обозначения: m1 – масса  - частицы,
- частицы,  – её скорость до рассеяния, m2 – масса дейтрона,
– её скорость до рассеяния, m2 – масса дейтрона,  1 и
1 и  2 – скорости
2 – скорости  - частицы и дейтрона соответственно после рассеяния.
- частицы и дейтрона соответственно после рассеяния.
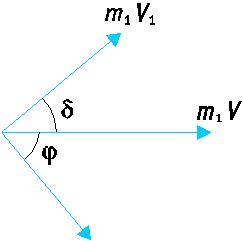
При отсутствии внешних сил в процессе упругого взаимодействия для системы «  - частица + дейтрон» сохраняются импульс (рис.40):
- частица + дейтрон» сохраняются импульс (рис.40):
m1V = m1V1  + m2 V2
+ m2 V2  , m1V1
, m1V1 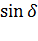 = m2 V2
= m2 V2  , и кинетическая энергия:
, и кинетическая энергия:  =
=  +
+  .
.
 .
.
Рис. 64.
Исключив из этих соотношений угол 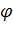 и величину V2 скорости дейтрона, получим квадратное уравнение для V1:
и величину V2 скорости дейтрона, получим квадратное уравнение для V1:
(m1 + m2) 
 2 m1VV1
2 m1VV1  + (m1
+ (m1  m2) V2 = 0.
m2) V2 = 0.
Корни этого уравнения будут вещественными при 
 . Максимальный угол
. Максимальный угол 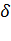 , удовлетворяющий этому условию, и есть искомый угол
, удовлетворяющий этому условию, и есть искомый угол  . Таким образом,
. Таким образом,
 = arc
= arc  =
= 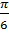 рад.
рад.
Заметим, что рассеяние на максимальный угол возможно только при условии: масса налетающей частицы больше массы покоящейся.
2).Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 65)
. 
Рис. 65. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние.
Решение
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей  1 и
1 и  2 после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 41), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
2 после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 41), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости 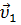 налетающего шара. Если массы шаров одинаковы, то векторы скоростей
налетающего шара. Если массы шаров одинаковы, то векторы скоростей  1 и
1 и  2 шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:
2 шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:  =
=  1 +
1 + 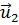 ;
;  =
=  +
+  .
.
Первое из этих равенств означает, что векторы скоростей  ,
,  1 и
1 и  2 образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами
2 образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами  1 и
1 и  2 равен 90°.
2 равен 90°.