 |
|
Уравнение с разделенными и разделяющимися переменными
Дифференциальное уравнение
(9)
называют уравнением с разделенными переменными.
Общий интеграл его есть
Пусть дифференциальное уравнение задано в форме (6) и каждая из функций 
состоит из произведений двух функций, каждая из которых зависит только от одной переменной, т.е.
и 
Тогда уравнение (6) записывается в виде
(10)
Уравнение вида (10) называется уравнением с разделяющимися переменными. Оно может быть приведено к уравнению с разделенными переменными путем деления обоих его частей на выражение 
:
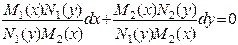
или 
т.е. к уравнению вида (9).
Если дифференциальное уравнение задано в виде (5), то оно называется уравнением с разделяющимися переменными,если 
представлено в виде
, т.е.
(11)
Это уравнение приводится к виду (9) путем деления обоих его частей на 
. Преобразуем, предполагая, что 
:
Интегрируя левую часть по 
, а правую по 
, получим:
Пример 1. Найти общее решение дифференциального уравнения
Решение. Интегрируя почленно, получим общий интеграл:
или 
Разрешая последнее уравнение относительно получим общее решение, т.е.
или 
(общее решение).
Пример 2. Найти решение уравнения
Решение. Данное уравнение представляет собой уравнение с разделяющимися переменными, т.е. уравнение вида (11).Разделив переменные, имеем:
Интегрируя, находим:
т.е. 
или 
(общий интеграл).
Разрешая последнее уравнение относительно , получаем общее решение 
.
Пример 3. Найти общее решение уравнения
Решение. Данное уравнение является уравнением с разделяющимися переменными. Путем деления обоих его частей на выражение 
получим:
Это уравнение с разделенными переменными. Интегрируя, получаем:
или 
(общий интеграл).
Отсюда получаем общее решение уравнения:
или 
.
Пример 4. Найти решение уравнения
Решение. Выражая производную функции через дифференциал 
получим уравнение:
.
Отсюда имеем: 
Разделяя переменные путем деления обеих частей на 
получим:
Интегрируя, имеем:
или
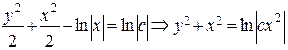(общий интеграл).