 |
|
Линейные уравнения первого порядка
Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Она имеет вид
(1)
где p(х) и q(x)- заданные неизвестные функции от х (или постоянные).
Если q(x)=0, то 
которое называется однородным линейным уравнением и она является уравнением с разделяющимися переменными.
Решение линейного уравнения (1) ищется в виде произведения двух неизвестных функций u(x) и v(x), т.е. y=uv. Учитывая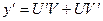 
и подставив значение у и у¢ через u и v в уравнение (1), получим:
или 
Так, как u и v произволные функции, то функцию v(x) выбираем так, чтобы выражение находящееся в скобке равнялось нулю, т.е.
. (2)
Это уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, находим частное решение v(x).
Тогда функция U(x) найдётся из уравнения
(3)
Тем самым решение исходного уравнения (1) сводится к решению двух уравнений с разделяющимися переменными (2) и (3).
Пример 1. Найти общее решение уравнения
Решение. Решение ищем в виде произведения двух функций u(x) и v(x). Таким образом, приняв y=uv и учитывая 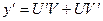, исходное уравнение представим в виде
или 
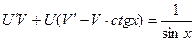(4)
Положим 
или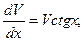 
откуда
Интегрируя, найдём какое либо частное решение этого уравнения, например, при с=0.
или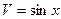 
.
При этом значении V(x), уравнение (4) примет вид:
или 
.
Решая это уравнение с разделяющимися переменными, получим
.
Тогда окончательно имеем
y=uv=(-ctgx+c)sinx или y=-cosx+csinx.
Пример 2. Найти общее решение уравнения
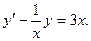
Решение. Пусть y=uv, т.е. 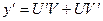. Тогда данное уравнение примет вид
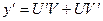или 
Для определения неизвестных функций u и v будем иметь в систему уравнений с разделяющимися переменными
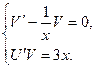
Решая первое уравнение, найдём какое- либо частное решение (с=0)
Учитывая v=x, из второго уравнения имеем:
; 
.
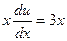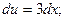
Тогда общее решение исходного уравнения:
y=uv= 
или 
.
Пример 3. Найти частное решение уравнения
удовлетворяющее начальному условию
у(0)=0.
Решение. Положим y=uv,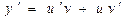 
. Тогда данное уравнение примет вид:
или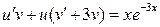 
.
Решим систему уравнений:
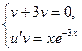
Из первого уравнения определим частное значение v(x):
Учитывая найденное значение v, из второго уравнения находим значение u(x), т.е.
откуда
Поэтому общее решение
.
Найдём частное решение, удовлетворяющее условию у=0 при х=0.
, т.е. с=0.
Таким образом, частное решение, удовлетворяющее заданному начальному условию, имеет вид:
.