 |
|
Дифференциальные уравнения первого порядка
Дифференциальные уравнения первого порядка, в общем случае, имеют вид
(4)
или 
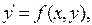(5)
здесь 
- искомая функция, 
- независимая переменная.
Иногда это уравнение записывается через дифференциалы зависимой и независимой переменных и 
в форме
(6)
где 
и 
- известные функции. Форма (6) удобна тем, что здесь переменные 
и 
равноправны.
Общим решением дифференциального уравнения первого порядка (4), (5), (6) называется функция
, (7)
а общим интегралом
Ф 
(8)
Для нахождения частного решения уравнения (4), (5), (6) задается начальное условие, например, 
при 
которое иногда записывается в виде 
Для определения частного решения данного дифференциального уравнения, удовлетворяющего начальному условию 
необходимо подставить значения 
и 
в уравнение (7), (8), найти значения 
и подставляя значения 
в уравнение (7), (8) найти частное решение.
Определение. Частным решением дифференциального уравнения первого порядка называется функция 
, которое получается из общего решения 
, если в последнем произвольному постоянному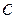 
придать определенное значение 
Соотношение Ф 
называется в этом случае частным интегралом уравнения.
Нахождение частного решение дифференциального уравнения называется задачей Коши.
Задача Коши. Найти решение 
дифференциального уравнения (5), удовлетворяющее заданному начальному условию: 
, т.е. принимающее при 
заданное значение 
.
Геометрически задача Коши формулируется так: найти интегральную кривую дифференциального уравнения (5), проходящую через заданную точку 
.
Не существует общего метода интегрирования дифференциального уравнения первого порядка. Обычно рассматривают лишь некоторые отдельные типы таких уравнений, для каждого из которых дается свой особый способ решения.