 |
|
Решение однородного уравнения
По условию f(tx,ty)=f(x,y). Положив в этом тождестве  получим:
получим:
 , (1¢)
, (1¢)
т.е. однородная функция нулевого измерения зависит только от отношения аргументов и однородное уравнение примет вид

Сделаем подстановку:
 т.е. y=Ux
т.е. y=Ux
тогда будем иметь:
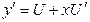 или
или 
Подставив это выражение производной в уравнение (1¢), получим:

Это уравнение с разделяющимися переменными.
 или
или 
Интегрируя, найдём:

Подставляя после интегрирования вместо U отношение  , получим интеграл уравнения (1¢).
, получим интеграл уравнения (1¢).
Пример 3. Найти общий интеграл уравнения

Решение. Приводим данное уравнение к виду

и определяем однородность функции f(x,y), т.е.

Здесь  и
и 
Поэтому функция f(x,y)- однородная функция нулевого измерения, т.е. дифференциальное уравнение однородное. Сделаем подстановку  или
или  т.е.:
т.е.:

 или
или 
Разделяя переменные будем иметь:

Отсюда, интегрируя, находим:
 ;
; 



Подставляя  , получим общий интеграл исходного уравнения:
, получим общий интеграл исходного уравнения:

Отсюда получим:

Пример 4. Решить уравнение
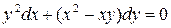
Решение. Решая данное уравнение относительно  , получим
, получим

Функция  является однородной функцией нулевого измерения. Поэтому данное дифференциальное уравнение однородное. Сделаем подстановку
является однородной функцией нулевого измерения. Поэтому данное дифференциальное уравнение однородное. Сделаем подстановку
 , т.е. у=Ux.
, т.е. у=Ux.
Тогда будем иметь:
 или
или 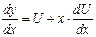
Подставим это выражение в дифференциальное уравнение  получим:
получим:
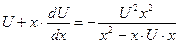 или
или  т.е.
т.е. 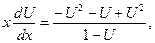

Разделив переменные, имеем
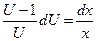
Интегрируя это уравнение, получим:
 ;
;  ; u-lnu-lnc=lnx;
; u-lnu-lnc=lnx;
u-lnu=lnxc.
Заменяя в последнем равенстве u отношением  , окончательно находим общий интеграл данного уравнения
, окончательно находим общий интеграл данного уравнения
 -ln
-ln 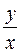 =lncx.
=lncx.
Пример 5. Решить уравнение

Решение. Так как функции находящиеся при dx и dy являются однородными функциями нулевого измерения то по определению данное уравнение однородное.
Разрешим данное уравнение относительно производной:
 или
или  .
.
Введя новую переменную  и учитывая у=ux,
и учитывая у=ux, 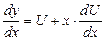 из последнего уравнения имеем:
из последнего уравнения имеем:
 .
.
Разделяя переменные и интегрируя почленно, получим:
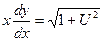 ;
; 
 или
или  .
.
Выполняя обратную замену, т.е.  , получим общий интеграл данного уравнения:
, получим общий интеграл данного уравнения:

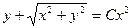 .
.
Пример 6. Найти частное решение уравнения
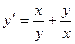
удовлетворяющее начальному условиюу=1 при х=1.
Решение. Данное уравнение однородное. Введя новую переменную  , учитывая у=ux и
, учитывая у=ux и  , данное уравнение преобразуется в уравнение с разделяющимися переменными:
, данное уравнение преобразуется в уравнение с разделяющимися переменными:
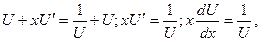
откуда 
Интегрируя это уравнение, получим
 .
.
Выполнив обратную замену, имеем
 .
.
Используя начальное уравнение у=1 при х=1 найдём значение производной постоянной С, т.е.
 2lnС=1, lnC=
2lnС=1, lnC=  ,
,  или
или 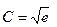 .
.
Тогда общее решение запишется в виде
 .
.
Пример 7. Решить уравнение

Решение. Данное уравнение представим в виде

Введя новую переменную  , учитывая у=ux и
, учитывая у=ux и  , получим уравнение с разделяющимися переменными:
, получим уравнение с разделяющимися переменными:

откуда 
Интегрируя это уравнение, получим
 или 1+U=Cx, U=Cx-1.
или 1+U=Cx, U=Cx-1.
Заменив в последнем равенстве U отношением  , находим общее решение данного уравнения:
, находим общее решение данного уравнения:
 или
или 
В задачах 1-15 найти общие интегралы (общее решение) уравнений.
1. 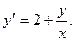 Ответ:
Ответ: 
2. (x+y)dx+2xdy=0. Ответ: x(x+3y)²=C
3.  Ответ:
Ответ: 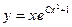
4.  Ответ:
Ответ:  .
.
5.  Ответ:
Ответ:  .
.
6. y²dx+(x²-xy)dy=0. Ответ:  .
.
7.  Ответ: x²+y²=Cx²y².
Ответ: x²+y²=Cx²y².
8. yy¢=2y-x. Ответ:  .
.
9.  . Ответ:
. Ответ: 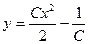 .
.
10. (x-y)ydy-x²dy=0. Ответ:  .
.
11. 2xyy¢=x²+y². Ответ: x²-y²=Cx.
12.  Ответ:
Ответ:  .
.
13.  Ответ:
Ответ:  .
.
14. (x²+y²)dx-2xydy=0. Ответ: (x-С)² -y²=C².
15.  . Ответ:
. Ответ:  .
.