 |
|
Уравнение второго порядка, не содержащее искомой функции
НЕДЕЛЯ 12
Лекция 23
Уравнения высших порядков
Дифференциальные уравнения высших порядков, допускающие
Понижение порядка
Простейшим уравнением n-го порядка является уравнение вида
y(n)=f(x). (1)
Данное уравнение решается последовательным n-кратным интегрированием. Интегрируя по х левые и правые части и принимая во внимание, что
y(n)=(у(n-1))¢, получим:
у(n-1) = 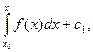
где х0- любое фиксированное значение х, а с1- постоянная интегрирования, и т.д. При каждом интегрировании получается одна произвольная постоянная, а в окончательном результате- n произвольных постоянных.
Пример1. Решить уравнения

Решение. Последовательно интегрируя, имеем
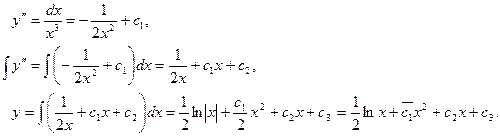
Пример 2. Найти общее решение уравнения
y¢¢=sin(kx)
и частное решение, удовлетворяющее начальным условиям
у(0)=0, у¢(0)=1.
Решение. Последовательно интегрируя данное уравнение имеем
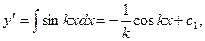
 .
.
Это есть общее решение. Чтобы найти частное решение, удовлетворяющее данным начальным условиям, достаточно определить соответствующие значения с1 и с2. Из условия у(0)=0 находим с2=0. Из условия у¢(0)=1 находим с1=1.Таким образом, искомое частное решение имеет вид

или
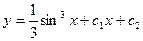 .
.
Уравнение второго порядка, не содержащее искомой функции
Рассмотрим уравнение вида
 ,
,
которое не содержит искомую функцию у.
Данное уравнение при помощи подстановки  и с учётом
и с учётом 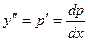 , преобразуется в уравнение первого порядка
, преобразуется в уравнение первого порядка
 .
.
Пример 1. Найти общее решение уравнения
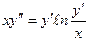 .
.
Решение. Данное уравнение не содержит искомую функцию у. Положим  , тогда
, тогда 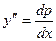 . Поэтому искомое уравнение преобразуется к вмду
. Поэтому искомое уравнение преобразуется к вмду
 или
или  .
.
Таким образом, мы получили однородное уравнение первого порядка. Для его решения воспользуемся подстановкой 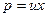 , откуда
, откуда 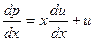 и следовательно, приходим к уравнению
и следовательно, приходим к уравнению
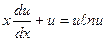 или
или 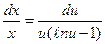 .
.
Интегрируя, получаем
 ,
,
откуда 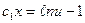 , т.е.
, т.е.  .
.
Возвращаясь к переменной у, имеем
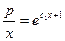 или
или 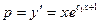 .
.
Остаётся проинтегрировать полученное уравнение первого порядка:
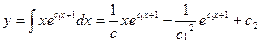 .
.
Пример 2. Найти частные решения уравнения

удовлетворяющее начальным условиям  ,
, 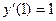 .
.
Решение. Данное уравнение не содержит искомую функцию у. Положив  ,
,  , получим уравнение с разделяющимися переменными.
, получим уравнение с разделяющимися переменными.
 .
.
Разделяя переменные и интегрируя, находим общее решение

Отсюда,  .
.
Используя начальные условия  ,
, 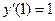 получим систему уравнений, для определения значений С1 и С2.
получим систему уравнений, для определения значений С1 и С2.

Отсюда, 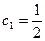 ,
,  .
.
Поэтому искомым частным решением исходного уравнения является
 .
.