 |
|
В задачах 1-20 найти общие интегралы (общие решения) уравнений.
. 
.
.
.
.
.
.
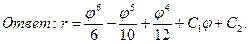
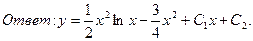
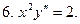
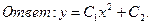
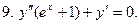
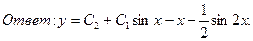
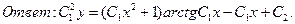
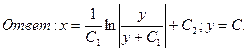
В задачах 21-27 найти частные интегралы (частные решения) уравнений, удовлетворяющие указанным начальным условиям.
21. 
22. 
23. 
24. 
25. 
26. 
27. 
Практическое занятие 24
Линейным однородным дифференциальным уравнением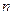 
-го порядка с постоянными коэффициентами называется уравнение
(1)
где коэффициенты 
- постоянные.
Общее решение линейного однородного уравнения (1)имеет вид
(2)
где 
- линейно независимые частные решения (фундаментальная система решений) этого уравнения, а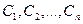 
- произвольные постоянные
Для отыскания общего решения уравнения (1) составляется характеристическое уравнение
(3)
Тогда общее решение уравнения (1) строится в зависимости от характера корней уравнения (3):
1) каждому действительному однократному (т.е. простому) корню 
в общем решении соответствует слагаемое вида 
2) каждому действительному корню 
кратностью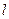 
в общем решении соответствует слагаемое вида
3) каждой паре комплексных напряженных однократных корней 
и 
в общем решении соответствует слагаемое вида
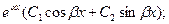
4) каждой паре комплексных сопряженных корней и 
кратности 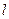в общем решении соответствует слагаемое вида
Пример 1. Найти общее решение уравнения
Решение. Составим характеристическое уравнение: 
Раскладывая левую часть уравнения на множители, имеем:
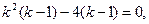или 
Следовательно, 
Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения имее вид:
Пример 2. Найти общее решение уравнения
Решение. Составим характеристическое уравнение: 
Раскладывая левую часть на множители, имеем:
Решая, находим: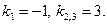 
Таким образом, характеристическое уравнение имеет один простой и один двукратный корень. Следовательно, общее решение дифференциального уравнения запишется в таком виде:
В задачах 1-15 найти общие решения уравнений.
1. 
2. 
.
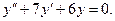
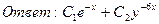3. 
.
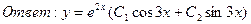4. 
5. 
6. 
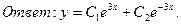
7. 
.
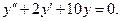
8. 
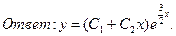
9. 
10. 
11. 
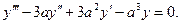
12. 
13. 
14. 
15. 
