 |
|
Практическое занятие 23
Пример 1. Найти общее решение уравнения
.
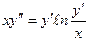Решение. Данное уравнение не содержит искомую функцию у. Положим 
, тогда 
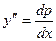. Поэтому искомое уравнение преобразуется к вмду
или 
.
Таким образом, мы получили однородное уравнение первого порядка. Для его решения воспользуемся подстановкой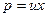 
, откуда 
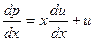и следовательно, приходим к уравнению
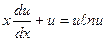или 
.
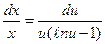Интегрируя, получаем
,
откуда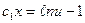 
, т.е. 
.
Возвращаясь к переменной у, имеем
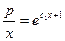или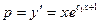 
.
Остаётся проинтегрировать полученное уравнение первого порядка:
.
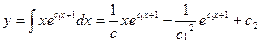Пример 2. Найти частные решения уравнения
удовлетворяющее начальным условиям 
, 
.
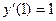Решение. Данное уравнение не содержит искомую функцию у. Положив 
, 
, получим уравнение с разделяющимися переменными.
.
Разделяя переменные и интегрируя, находим общее решение
Отсюда, 
.
Используя начальные условия 
, 
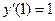получим систему уравнений, для определения значений С1 и С2.
Отсюда,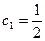 
, 
.
Поэтому искомым частным решением исходного уравнения является
.
Пример 3. Найти общее решение уравнения
.
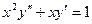Решение. Положим , 
. Тогда,
.
Последнее уравнение является линейным уравнением. Поэтому решение принимаем в виде произведения u(x) и v(x), т.е.p=uv, 
.
Тогда, используя эти выражения и решая полученное уравнение, имеем
Отсюда, 
, 
или 
Учитывая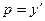 
и решая полученное уравнение, получим:
, т.е.
.
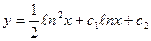Уравнение второго порядка, не содержащее независимой
Переменной
Рассмотрим уравнение вида
,
которое не содержит независимую переменную х. Для его решения снова положим
,
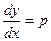где p=p(y). Тогда 
.
Подставляя эти выражения в исходное уравнение, получим
.
Интегрируя его, найдём р как функцию от у и произвольного постоянного с1:
.
Учитывая 
, получим 
Разделяя переменные и интегрируя, получим общим интеграл исходного уравнения:
.
Пример 1. Найти общее решение уравнения
2уу¢¢=(у¢)2.
Решение. Положим у¢=р, у¢¢=р×р¢, где р=р(у). Тогда исходное уравнение будет иметь вид:
2у×р×р¢=р2 или 2у×р¢=р, Þ 
Разделяя переменные и интегрируя, получим
Учитывая у¢=р и интегрируя, имеем
или
Пример 2. Найти общий интеграл уравнения
у¢¢tgy=2(y¢)².
Решение. Данное уравнение не содержит независимую переменную х. Поэтому применим подстановку у¢=р, у¢¢=р×р¢, и данное уравнение преобразуется к виду
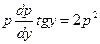или 
Интегрируя почленно, находим
или р=С1sin2y.
Заменяя р на 
, получим
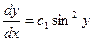или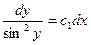 
,
откуда находим общий интеграл данного уравнения
-ctgy=c1x+c2.