Главная | Обратная связь

Определения и общие свойства

Определение. Дифференциальные уравнения n-го порядка называется линейным, если оно первой степени относительно искомой функции и её производных т.е. имеет вид

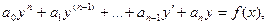(1)

где и f(x)- заданные функции от х или постоянные, причем для всех значений х из той области, в которой мы рассматриваем уравнение (1). В дальнейшем мы будем предполагать, что функции 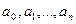и f(x) непрерывны при всех значениях х, причем (если он не равен 1, мы можем все члены уравнения поделить на него).

Функция f(x), стоящая в правой части уравнения, называется правой частью уравнения.

Если , то уравнение называется линейным неоднородным, а если же f(x)=0, то линейным однородным, т.е.

- линейное неоднородное

Линейные однородные дифференциальные уравнения второго

Порядка

Теорема 1. Если у₁ и у₂ –два частных решения линейного однородного уравнения второго порядка

(3)

то у₁ +у₂ есть также решение этого уравнения.

Теорема 2. Если у₁ есть решение уравнения (3) и с- постоянная, то с у₁ есть также решения уравнения (3).

Определение. Два решения уравнения (3) у₁ и у₂ называются линейно независимыми на отрезке [a,b], если их отношения на этом отрезке не являются постоянным, т.е. если

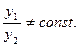
В противном случае решения называются линейно зависимыми. Иначе говоря, два решения 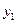и называются линейно зависимыми на отрезке , если существует такое постоянное число 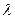, что при В этом случае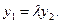

 

Пример 1. Пусть имеем уравнение Функции являются решениями. При этом функции и линейно независимы, т.к. не остается постоянным при изменении х. Функции же и линейно зависимы, т.к.

Определение. Если у₁ и у₂ есть функции от х, то определитель

называется определителем Вронского или вронскианом данных функции.

Теорема 3. Если 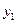и - линейно зависимы на отрезке , то определитель Вронского на этом отрезке тождественно равны нулю.

Теорема 4. Если определитель Вронского W(у₁,у₂) составленный для решений у₁ и у₂ линейного однородного уравнения (3), не равен нулю при каком-нибудь значении х=х₀ на отрезке , где коэффициенты уравнения непрерывны, то он не обращается в нуль ни при каком значении х на этом отрезке и .

Теорема 5. Есл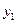и и - два линейно независимых частных решении линейного однородного уравнения второго порядка (3), то общее решение уравнения есть линейная комбинация этих частных решений, т.е. общее решение уравнения (3) имеет вид

где и 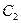- произвольные постоянные.

Итак, чтобы найти общее решение уравнения (3), достаточно знать два его частных линейно независимых решени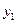й и .

Пример 2.Уравнени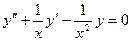е ,гденепрерывно на любом отрезке,не содержащем точку х=0, допускает частное решение у₁=х,

У₂= _. Следовательно, его общее решение

.