 |
|
Линейные неоднородные дифференциальные уравнения второго
Неделя 13
Лекция 25
Линейные однородные уравнения второго порядка с постоянными
Коэффициентами
Имеем линейное однородное дифференциальное уравнение
 (1)
(1)
где  и
и 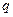 - постоянные действительные числа. Чтобы найти общий интеграл этого уравнения, найдем два линейно независимых частных решения.
- постоянные действительные числа. Чтобы найти общий интеграл этого уравнения, найдем два линейно независимых частных решения.
Будем искать частные решения в виде
 где
где  . (2)
. (2)
Тогда
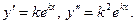
Подставляя  в уравнение (1), получим:
в уравнение (1), получим:

Так как 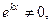 то
то  (3)
(3)
Уравнение (3) называется характеристическим уравнением уравнения (1).
Решая характеристическое уравнение (3), получим

Здесь могут представиться три различных случая.
Случай 1. Корни характеристического уравнения действительны и различны: 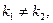 если
если  В этом случае частными решениями будут функции
В этом случае частными решениями будут функции
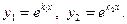
Эти решения линейно независимы, так как

Следовательно, общий интеграл имеет вид
 .
.
Пример 1. Решить уравнение
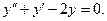
Решение. Характеристическое уравнение имеет вид
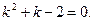
Решая его, находим его корни: 
Тогда общее решение исходного уравнения имеет вид

Пример 2. Решить уравнение
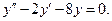
Решение. Решая характеристическое уравнение

Находим его корни: 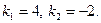 Общее решение исходного уравнения имеет вид
Общее решение исходного уравнения имеет вид
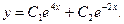
Случай 2. Корни характеристического уравнения действительные и равные: 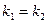 при
при 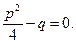
Тогда 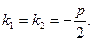 Поэтому одно частное решение уравнения (1) будет
Поэтому одно частное решение уравнения (1) будет 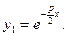
Всякое другое частное решение 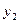 , линейно независимое с
, линейно независимое с  , обязательно должно иметь вид
, обязательно должно иметь вид
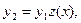
где 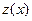 - некоторая функция от
- некоторая функция от  не являющаяся тождественно постоянной. Отсюда
не являющаяся тождественно постоянной. Отсюда
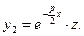
Дифференцируя 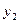 по
по  дважды и подставляя
дважды и подставляя 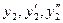 в уравнение (1) и сокращая на общий множитель
в уравнение (1) и сокращая на общий множитель  а также решая, получим
а также решая, получим
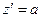 и
и 
где 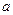 и
и 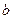 - произвольные постоянные. Следовательно,
- произвольные постоянные. Следовательно,
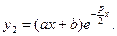
Так как мы интересуемся частным решением, то можно принять  и
и 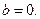 Тогда
Тогда 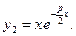
Таким образом, общее решение уравнения (1) будет функция
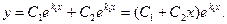
Пример 1. Решить уравнение
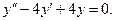
Решение. Корнями характеристического уравнения

являются 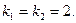 Тогда общее решение исходного уравнения запишется в виде
Тогда общее решение исходного уравнения запишется в виде

Случай 3. Корни характеристического уравнения – комплексные.
Так как комплексные корни входят попарно сопряженными, то обозначим:

где 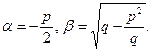
Частные решения можно записать в форме:
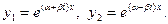
Отсюда, окончательно получим:

где 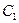 и
и 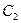 - произвольные постоянные.
- произвольные постоянные.
Пример 1. Дано уравнение
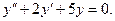 Найти общий интеграл и частное решение, удовлетворяющее условиям:
Найти общий интеграл и частное решение, удовлетворяющее условиям: 
Решение. Напишем характеристическое уравнение

И найдем его корни: 
Следовательно, общий интеграл: 
Найдем частное решение, удовлетворяющее данным начальным условиям, и определим значения 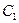 и
и  На основании первого условия находим:
На основании первого условия находим:
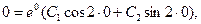 откуда
откуда 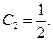
Таким образом, искомое частное решение есть

Пример 2. Дано уравнение

Найти общий интеграл и частное решение, удовлетворяющее начальным условиям 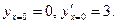
Решение. Напишем характеристическое уравнение

Находим его корни:

Общий интеграл есть
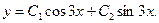
Найдем частное решение. Предварительно найдем: 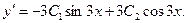
Постоянные 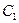 и
и 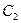 определяются из начальных условий:
определяются из начальных условий:


Они равны: 
Частное решение: 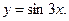
Линейные однородные уравнения  -го порядка с постоянными
-го порядка с постоянными
Коэффициентами
Линейным однородным дифференциальным уравнением  -го порядка с постоянными коэффициентами называется уравнение
-го порядка с постоянными коэффициентами называется уравнение
 (1)
(1)
где коэффициенты  - постоянные.
- постоянные.
Общее решение линейного однородного уравнения (1)имеет вид
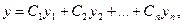 (2)
(2)
где 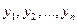 - линейно независимые частные решения (фундаментальная система решений) этого уравнения, а
- линейно независимые частные решения (фундаментальная система решений) этого уравнения, а 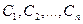 - произвольные постоянные
- произвольные постоянные
Для отыскания общего решения уравнения (1) составляется характеристическое уравнение
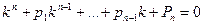 (3)
(3)
Тогда общее решение уравнения (1) строится в зависимости от характера корней уравнения (3):
1) каждому действительному однократному (т.е. простому) корню 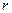 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 
2) каждому действительному корню 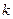 кратностью
кратностью  в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида

3) каждой паре комплексных напряженных однократных корней 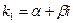 и
и  в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида

4) каждой паре комплексных сопряженных корней 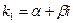 и
и 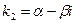 кратности
кратности  в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида
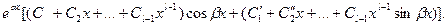
Пример 1. Найти общее решение уравнения
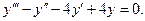
Решение. Составим характеристическое уравнение:  Раскладывая левую часть уравнения на множители, имеем:
Раскладывая левую часть уравнения на множители, имеем:
 или
или 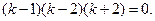
Следовательно,  Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения имее вид:
Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения имее вид:

Пример 2. Найти общее решение уравнения

Решение. Составим характеристическое уравнение: 
Раскладывая левую часть на множители, имеем:
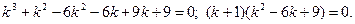
Решая, находим:  Таким образом, характеристическое уравнение имеет один простой и один двукратный корень. Следовательно, общее решение дифференциального уравнения запишется в таком виде:
Таким образом, характеристическое уравнение имеет один простой и один двукратный корень. Следовательно, общее решение дифференциального уравнения запишется в таком виде:
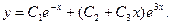
Пример 3. Найти общее решение уравнения 
Решение. Этому уравнению соответствует характеристичсекое уравнение:  или
или 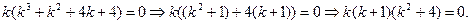
Отсюда,  Характеристичсекое уравнение имеет два действительных и два комплексных корня (все они простые).
Характеристичсекое уравнение имеет два действительных и два комплексных корня (все они простые).
Общее решение дифференциального уравнения запишется в виде:

Пример 4. Найти общее решение уравнения

Решение. Данному уравению соответствует арактеристичсекоеуравнение:  или
или 
имеющее двукратные комплексные корни  Следовательно, общее решение дифференциального уравнения записывается в таком виде:
Следовательно, общее решение дифференциального уравнения записывается в таком виде:

Лекция 26
Линейные неоднородные дифференциальные уравнения второго