Главная | Обратная связь

Порядка с постоянными коэффициентами

 

Линейное неоднородное дифференциальное уравнение второго порядка имеет вид

. (1)

Оно отличается от соответствующего линейного однородного уравнения

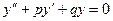(2)

наличием в правой части некоторой функции f(x).

Для нахождения общего решения уравнения (1) сначала нужно найти общее решение 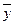уравнения(2), а затем найти какое-либо частное решение данного неоднородного уравнения(1):

Выше было указано на общий метод нахождения частных решений неоднородного уравнения, т.е. метод вариации произвольных постоянных .

В случае уравнения с постоянными коэффициентами, частное решение иногда бывает возможно найти проще, не прибегая к интегрированию(метод неопределённых коэффициентов). Рассмотрим несколько таких возможностей для уравнения(1).

1.Пусть правая часть уравнения (1) имеет вид

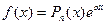, (3)

где - многочлен n-ой степени. Тогда возможны следующие частные случаи:

a) число 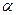не является корнемхарактеристического уравнения

.

В этом случае частное решение нужно искать в виде

, (4)

где 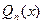-многочлен степени n, с неизвестными коэффициентами. Для того чтобы найти коэффициент многочленов 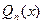, искомое частное решение (4) подставляют в левую часть уравнения (1) и производят соответствующие упрощения; затем в полученном тождестве приравнивают коэффициенты при подобных членах в левой и правой частях, что даёт систему линейных уравнений относительно искомых коэффициентов, из которой определяют эти коэффициенты.

б ) число 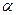есть простой (однородный) корень характеристического уравнения. В этом случае частное решение нужно искать в виде

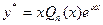. (5)

в ) число 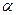- есть двукратный корень характеристического уравнения.

В этом случае:

. (6)

Пример 1. Найти общее решение уравнения

Решение. характеристическое уравнение имеет решение 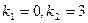, то общее решение соответствующего однородного уравнения есть

.

Так как правая часть данного неоднородного уравнения имеет вид

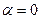и является простым корнем характеристического уравнения то частное решение ищем в виде

.

Подставляя это выражение в дифференциальное уравнение будем иметь:

2A-3(2Ax+B)=1+6x или -6Ax+2A-3B=1+6x

Приравнивая коэффициенты при одинаковых степенях х, получим:

.

Откуда А=-1, В=-1. Следовательно, частное решение

.

И общее решение

.

Пример 2.Найти общее решение уравнения

.

Решение. Характеристическое уравнение. 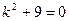, соответствующего однородного уравнения имеет решение

Тогда общее решение соответствующего однородного уравнения:

.

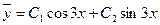Правая часть заданного уравнения 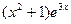и не является корнем характеристического уравнения, это частное решение ищем в виде:

.

Подставляя это выражение в дифференциальное уравнение, будем иметь:

.

Сокращая на 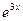и приравнивая коэффициенты при одинаковых степенях х, получим:

Откуда 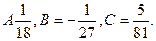Следовательно, частное решение

.

И общее решение

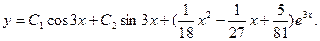
Пример 3 . Найти частное решение уравнения

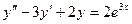
Решение.Характеристическое уравнение 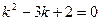имеет корни

и не является корнем.

Таким образом, частное решение ищем в виде

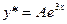
Подставляя это выражение в данное уравнение, будем иметь

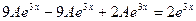или 2А=2.

Поэтому А=1 и искомое частное решение

.

Пример 4 . Найти общее решение уравнения

Решение. Характеристическое уравнение 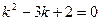имеет решение и является простым корнем характеристического уравнения, поэтому общее решение соответствующего однородного уравнения 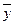и частное решение ищем в виде:

, .

Подставляя в данное уравнение, будем иметь:

,

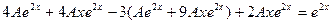или (сокращая на и объединяя подобные члены)

Отсюда А=1 и частное решение имеет вид:

.

Общее решение данного неоднородного уравнения:

.

Пример 5. Найти частное решение уравнения

Решение. В данном случае и является корнями характеристического уравнения 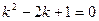следовательно является 2 кратным корнем. Поэтому частное решение ищем в виде:

.

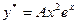Подставляя это выражение в данное дифференциальное уравнение, имеем

Отсюда, 2А=6 и А=3.

Поэтому частным решением является:

.