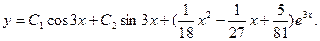Главная | Обратная связь

Пусть правая часть уравнения (1) имеет вид

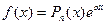, (3)

где - многочлен n-ой степени. Тогда возможны следующие частные случаи:

a) число 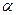не является корнемхарактеристического уравнения

.

В этом случае частное решение нужно искать в виде

, (4)

где 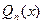-многочлен степени n, с неизвестными коэффициентами. Для того чтобы найти коэффициент многочленов 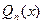, искомое частное решение (4) подставляют в левую часть уравнения (1) и производят соответствующие упрощения; затем в полученном тождестве приравнивают коэффициенты при подобных членах в левой и правой частях, что даёт систему линейных уравнений относительно искомых коэффициентов, из которой определяют эти коэффициенты.

б ) число 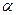есть простой (однородный) корень характеристического уравнения. В этом случае частное решение нужно искать в виде

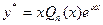. (5)

в ) число 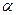- есть двукратный корень характеристического уравнения.

В этом случае:

. (6)

Пример 1. Найти общее решение уравнения

Решение. характеристическое уравнение имеет решение 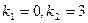, то общее решение соответствующего однородного уравнения есть

.

Так как правая часть данного неоднородного уравнения имеет вид

и 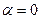является простым корнем характеристического уравнения то частное решение ищем в виде

.

Подставляя это выражение в дифференциальное уравнение будем иметь:

2A-3(2Ax+B)=1+6x или -6Ax+2A-3B=1+6x

Приравнивая коэффициенты при одинаковых степенях х, получим:

.

Откуда А=-1, В=-1. Следовательно, частное решение

.

И общее решение

.

Пример 2.Найти общее решение уравнения

.

Решение. Характеристическое уравнение. 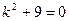, соответствующего однородного уравнения имеет решение

Тогда общее решение соответствующего однородного уравнения:

.

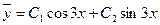Правая часть заданного уравнения 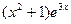и не является корнем характеристического уравнения, это частное решение ищем в виде:

.

Подставляя это выражение в дифференциальное уравнение, будем иметь:

.

Сокращая на 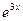и приравнивая коэффициенты при одинаковых степенях х, получим:

Откуда 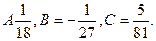Следовательно, частное решение

.

И общее решение