 |
|
Пусть правая часть имеет вид
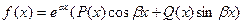(7)
Где P(x) и Q(x) – многочлены от х , это форма от частного решения зависящее от правой части определяется так:
а ) если число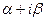 
не является корнем характеристического уравнения, это частное решение уравнения(1) следует искать в виде
, (8)
где u(x) и v(x)- многочлены, степень которых равна наивысшей степени многочленов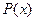 
и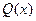 
;
б ) если число 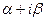есть корень характеристического уравнения, это частное решение ищем в виде
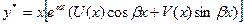, (9)
где u(x) и v(x)- многочлены, степень которых равна наивысшей степени многочленов 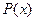и ;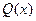
Указанные формы частных решений (8) и (9), сохраняются и в этом случае, когда в правой части уравнения (7) один из многочленов 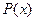и 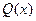тождественно равен нулю, т.е. когда первая часть имеет вид
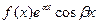или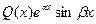 
.
Полезно рассмотреть отдельно , важный частный случай, т.е. когда правая часть линейного уравнения второго порядка имеет вид
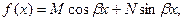(10)
где M,N-постоянные числа.
а ) Если 
i не является корнем характеристического уравнения, это частное решение следует искать в виде
. (11)
б ) Если i 
является корнем характеристического уравнения, это частное решение следует искать в виде
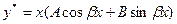. (12)
Отметим, что функция (10) является частным случаем функции (7)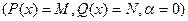 
; функции (11) и (12) являются частными случаями функции (8) и (9)
Пример 3.Найти общее решение уравнения
.
Решение. Находим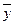 
. Характеристическое уравнение 
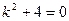имеет корни 
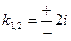. Следовательно:
.
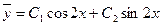Переходим к отысканию частного решения отвечающее правой части данного уравнения, которая имеет вид (7), где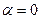 
, P(x)=3x,Q(x)=0
Число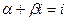 
не является корнем характеристического уравнения.
Поэтому частное решение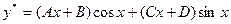 
, где A,B,C,D –неопределённые коэффициенты. Дифференцируя, находим
.
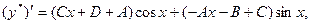
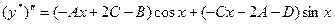Подставим выражения 
и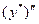 
в данное уравнение и сгруппируя члены при cosx и sinx, получим
.
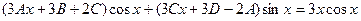Сравнивая коэффициенты при xcosx, cosx, xsinx и sinx, имеем
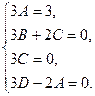
Решая систему уравнений имеем А=1, B=0,C=0,D= 
Таким образом,
.
Итак, общее решение данного уравнения имеет вид:
.
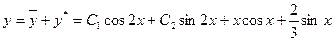Пример 4. Найти общее решение уравнения
.
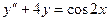Решение. Характеристическое уравнение имеет корни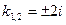 
. Поэтому общее решение соответствующего однородного уравнения имеет вид
.
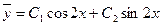Частное решение неоднородного уравнения ищем в виде (9), т.к. 
и число 
является однородным корнем характеристического уравнения. Таким образом:
.
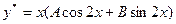Тогда,
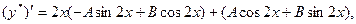
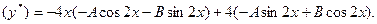
Подставляя эти выражения производных в данное уравнение и приравнивая коэффициенты при cos2x и sin2x, получаем систему уравнений для определения A и B: 4В=1, -4А=0, откуда А=0, В= 
. Таким образом:
.
Итак, общее решение этого уравнения имеет вид
.