Главная | Обратная связь

Теоретические основы конечно-элементного анализа

Метод конечных элементов представляет собой эффективныйчисленный метод решения инженерных и физических задач. Область его применения простирается от анализа напряжений в конструкциях самолетов или автомобилей до расчета таких сложных систем, как атомная электростанция. С его помощью рассматривается движение жидкости по трубам, через плотины, в пористых средах, исследуется течение сжимаемого газа, решаются задачи электростатики и смазки, анализируются колебания систем.

Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.

 

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения.

В настоящее время область применения метода конечных элементов очень обширна и охватывает все физические задачи, которые могут быть описаны дифференциальными уравнениями.

Наиболее важными преимуществами метода конечных элементов, благодаря которым он широко используется, являются следующие:

– Свойства материалов смежных элементов не должны быть обязательно одинаковыми. Это позволяет применять метод к телам, составленным из нескольких материалов;– Криволинейная область может быть аппроксимирована с помощью прямолинейных элементов или описана точно с помощью криволинейных элементов. Таким образом, методом Можно пользоваться не только для областей с «хорошей» формой границы;– Размеры элементов могут быть переменными. Это позволяет укрупнить или измельчить сеть разбиения области на элементы, если в этом есть необходимость;– С помощью метода конечных элементов не представляет труда рассмотрение граничных условий с разрывной поверхностной нагрузкой, а также смешанных граничных условий;– Указанные выше преимущества метода конечных элементов могут быть использованы при составлении достаточно общей программы для решения частных задач определенного класса.Главный недостаток метода конечных элементов заключается к необходимости составления вычислительных программ и применения вычислительной техники. Вычисления, которые требуетсяпроводить при использовании метода конечных элементов, слишком громоздки для ручного счета даже в случае решения очень простых задач. Стоит отметить, что метод конечных элементов, конечно, является приближенным численным методом, и тем самым имеет некоторую степень погрешности. Однако, в нем заложено большое количество параметром с помощью которых можно управлять степенью точности получаемых результатов (измельченность сетки, параметры нагружения и методов получения решения). Отдельным вопросом является степень адекватности решаемой математической модели ее физическому прототипу. Все это возлагается на плечи инженера-расчетчика, ответственность за результат несет только он. Но следует сказать, что МКЭ позволяет исследовать конструкции почти неограниченной степени сложности. В то время как это объективно невозможно с использованием аналитических методов.Основная идея метода конечных элементов (МКЭ) состоит в том, что любая непрерывная величина (температура, давление, перемещение) аппроксимируется дискретной моделью, построение которой выполняется на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Алгоритм построения дискретной модели изучаемой непрерывной величины заключается в следующем:– В рассматриваемой области фиксируют конечное число точек. Эти точки в дальнейшем называют узлами;– Полагают, что исследуемая непрерывная величина в каждом узле является переменной, подлежащей определению в процессе решения задачи;– Область изменения непрерывной величины разбивают на элементы. Эти элементы имеют между собой общие узлы и, в совокупности, аппроксимируют форму области в целом;– Непрерывную величину аппроксимируют в пределах каждого элемента полиномом, коэффициенты которого рассчитывают на основании значений этой величины в узлах. Каждый элемент аппроксимируют своим полиномом, а коэффициенты полиномов подбирают таким образом, чтобы сохранялась непрерывность величины вдоль границ соседних элементов.

Фундаментальный принцип МКЭ заключается в разбиении изучаемой области на элементарные области конечных размеров (конечные элементы) [18]. В каждом таком элементе неизвестная функция аппроксимируется полиномом, степень которого меняется в зависимости от аппроксимируется задачи, но остается обычно невысокой (от 1 до 6). Для каждого элемента аппроксимирующий полином определяется его коэффициентами. Коэффициенты могут быть определены значениями функции в частных точках, называемых узлами элемента. Если известна функция в каждом узле, то имеется возможность ее аппроксимации на всей области. Можно также сказать, что неизвестная функция A(x,y,z) зависит от M параметров A₁, A₂, ..., A_M, являющихся неизвестными, которые функция принимает в каждом узле каждого элемента. Определение параметров A₁, A₂, ..., A_M является этапом определения A(x,y,z).

Зная вариационное представление задачи,

 

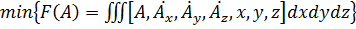, (1)

 

заменяют тройной интеграл на сумму интегралов на каждом конечном элементе области:

 

, (2)

 

где N_e - число элементов разбиения;

F_e - часть F на элементе с номером e.

На каждом элементе с номером e функция A может быть заменена ее аппроксимацией, интегрирование которой дает F(A) в виде функции одних только параметров элемента e.

Суммируя, получают:

 

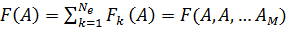. (3)

 

Принимая во внимание, что некоторые из узлов 1, 2, ...,M являются общими для нескольких элементов и что вклад каждого элемента должен учитываться в выражении для функции F относительно величин A₁, A₂, ..., A_M неизвестной функции в этих узлах, когда объединяют элементы для всей области.

Отыскивается оптимум F по всей области, имея в виду, что частные производные F относительно величин A₁, A₂, ..., A_M одновременно обращаются в нуль:

 

(4)

 

Эта операция приводит к составлению системы из M уравнений с M неизвестными, которые определяют величины A₁, A₂, ..., A_M в узлах разбиения. Правая часть этих уравнений получается, исходя из той части функционала, которая содержит в себе члены, характеризующие источники, или на основе значений А, заданных на границе области (неоднородные граничные условия-Дирихле).

При использовании МКЭ приходится вычислять определенные интегралы, когда на каждом элементе сети разбиения определяется элементарная матрица интегрированием на каждом элементе функционала, аппроксимируемого с помощью функций формы. Если же элементы криволинейны или задача нелинейна, аналитическое интегрирование становится невозможным и тогда приходится прибегать к численному интегрированию.

Использование МКЭ приводит к вычислению определенных интегралов на отрезках прямых, дуг кривых или в некоторых областях. При интегрировании по области можно использовать интегрирование по каждому ее элементу, тогда для интегралов, упомянутых выше, необходимо использовать эффективные и точные методы численного интегрирования.