 |
|
Выбор программного обеспечения. Описание и анализ возможностей программного комплекса ANSYS
Популярность МКЭ способствовала созданию различных коммерческих пакетов программ, среди которых можно отметить следующие часто используемые: NASTRAN, ASKA, MICROFLUX, GE2D, ANSYS.
Все пакеты, реализующие метод конечных элементов, состоят из информационной и вычислительной частей. Информационная часть – база данных (БД) пакета – содержит описания используемых данным пакетом типов элементов (библиотеку элементов), библиотеку материалов, справочную систему. Физически представляет собой набор файлов, расположенных в том каталоге, куда был установлен пакет.
Вычислительная часть пакетов МКЭ представляет собой набормодулей (называемых обычно процессорами), выполняющих определенныефункции и объединенных общей оболочкой (реализация этой идеи различнав разных пакетах – модули могут представлять собой отдельные EXE-файлы,либо входить в единый файл в виде подпрограмм). Среди процессоровобычно выделяют препроцессор (preprocessor) – модуль подготовкиисходных данных, вычислительный процессор – solver(или вычислительныепроцессоры – для пакетов, решающих широкий круг задач) и постпроцессор(postprocessor) – средство визуализации и анализа результатов расчета.
Стоит отметить, что настоящее время существует набор пакетов, моделирующих непосредственно структуру композиционных материалов. К сожалению, данные пакеты чаще всего имеют слабый геометрический модуль и дороги в финансовом плане. Зачастую пользователь таких пакетов сталкивается с проблемой моделирования сложных деталей и сборок, необходимостью их адаптации (в том числе длительного периода подготовки) и интеграции а также с проблемой ограниченности расчетного ресурса. Поэтому зачастую организации, занимающиеся расчетами, стремятся подобрать наиболее универсальный пакет, способный решать задачи различных областей. Одним из таких пакетов является ANSYS.
ANSYS - это универсальный конечно-элементный программный пакет (разработчиком которого является компания ANSYS Inc.), который позволяет решать в единой пользовательской среде (и, что очень важно, на одной и той же конечно-элементной модели) широкий круг задач в областях: прочности, тепла, гидрогазодинамики, электромагнетизма, междисциплинарного связанного анализа, объединяющего все четыре типа, оптимизации конструкции на основе всех вышеприведенных типов анализа [19].
ANSYS обеспечивает двустороннюю связь практически со всеми известными CAD-системами. Это достигается за счет двустороннего обмена геометрией с наиболее популярными пакетами и импорта множества стандартных-форматов.
Также существуют встраиваемые в CAD-системы расчетные модули ANSYS, позволяющие реализовать преимущества технологии "сквозного проектирования".
Новый релиз ANSYS включает в себя последние достижения CAE-технологий и обеспечивает инновационные передовые технологии моделирования в классе инженерных программных продуктов. Версия 12.1 включает в себя сложные типы анализа механических систем и конструкций, работу с геометрией, построение конечно-элементных (КЭ) сеток, многодисциплинарный анализ, контактные задачи, новые решатели для связанных задач и многое другое. Все эти улучшения – это большой шаг вперед в моделировании и разработке продуктов.
С улучшениями версии 12.1 возможность решать сложные задачи значительно увеличилась, появились:новые элементы: для дискретного армирования и моделирования нелинейных свойств материалов, и учета гиперупругости, Модель Ананда для задания вязкопластичности; Модель Друкера-Прагера с учетом ползучести; Модель материала Бергстрома-Бойса для описания свойств эластомеров; специализированный решатель Supernodesolver для расчета большого числа форм колебаний (до 10.000) для одного расчета - и их характеристики, новое семейство элементов для связанного анализа – моделирования протекания жидкости через пористую среду.
Еще одним улучшением ANSYS Workbench стало добавление прямого решателя для связанных задач.
В 12-й версии для коэффициента трения могут быть заданы зависимости от температуры, времени, нормального давления, расстояния скольжения, или относительной скорости скольжения. Также в новой версии можно использовать пользовательскую подпрограмму USERFRIC для задания пользовательской модели трения для двумерных и трехмерных контактных элементов.(CONTA171, CONTA172, CONTA173, CONTA174, CONTA175, CONTA176, CONTA177, CONTA178).
В релизе 12.1 расширены расчетные возможности ANSYS Workbench – появилась возможность записи, настройки и автоматизации этапов расчета с помощью журнала и скриптов. В журнале записываются данные о расчетах в ANSYS Workbench. Такой файл можно использовать повторно для возобновления сессии ANSYS Workbench. Кроме того, в журнал можно добавлять дополнительные операции, известные как scripting. Применение журнала и скриптов в ANSYS Workbench позволяет повторно использовать ранее созданные журналы или восстановить ранее созданные проекты, автоматизировать решение повторяющихся задач или проводить расчеты в пакетном режиме. С помощью платформы ANSYS Workbench можно легко использовать необходимые программные продукты в процессе проектирования. С помощью интуитивного интерфейса любой специалист, даже не занятый в процессе расчетов, может следить за тем, как идет процесс моделирования, какие инструменты используются и как происходит обмен данными.
1.5 Основные уравнения теории упругости . Типы задач теории упругости
Основная задача теории упругости – определение напряженно-деформированного состояния по заданным условиям нагружения и закрепления тела.
Напряженно-деформированное состояние определено, если найдены компоненты тензора напряжений {s} и вектора перемещений 
, девять функций.
1.5.1 Основные уравнения теории упругости
Для того, чтобы найти эти девять функций надо записать основные уравнения теории упругости, или:
Дифференциальные Коши
(17)
где - компоненты тензора линейной части деформаций Коши;
компоненты тензора производной перемещения по радиусу.
Дифференциальные уравнения равновесия
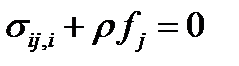(18)
где - компоненты тензора напряжений; - проекция объемной силы на ось j.
Закон Гука для линейно-упругого изотропного тела
(19)
где - константы Ламе; для изотропного тела. Здесь - нормальные и касательные напряжения; деформации и углы сдвига соответственно.
Вышеперечисленные уравнения должны удовлетворять зависимостям Сен-Венана
(20)
В теории упругости задача решена, если выполняются все основные уравнения.
1.5.2 Типы задач теории упругости
Граничные условия на поверхности тела должны выполняться и в зависимости от типа граничных условий различают три типа задач теории упругости.
Первый тип. На поверхности тела заданы силы. Граничные условия
Второй тип. Задачи, в которых на поверхности тела задано перемещение. Граничные условия
Третий тип. Смешанные задачи теории упругости. На части поверхности тела заданы силы, на части поверхности тела задано перемещение. Граничные условия
1.5.3 Прямая и обратная задачи теории упругости
Задачи, в которых на поверхности тела заданы силы или перемещения, а требуется найти напряженно-деформированное состояние внутри тела и то, что не задано на поверхности, называют прямыми задачами. Если же внутри тела заданы напряжения, деформации, перемещения и т.д., а требуется определить то, что не задано внутри тела, а также перемещения и напряжения на поверхности тела (то есть найти причины, вызвавшие такое напряженно-деформированное состояние) ), то такие задачи называются обратными.
1.5.4 Уравнения теории упругости в перемещениях (уравнения Ламе)
Для определения уравнений теории упругости в перемещениях запишем: дифференциальные уравнения равновесия (18) закон Гука для линейно-упругого изотропного тела (19)
(19)
Если учесть, что деформации выражаются через перемещения (17), запишем:
(22)
Следует также напомнить, что угол сдвига связан с перемещениями следующим соотношением (17):
(23)
Подставив в первое уравнение равенств (19) выражение (22), получим, что нормальные напряжения
(24)
Отметим, что запись иц в данном случае не подразумевает суммирования по i.
Подставив во второе уравнение равенств (19) выражение (23), получим, что касательные напряжения
(25)
Запишем уравнения равновесия (18) в развернутом виде для j = 1
(26)
Подставив в уравнение (26) выражения для нормальных (24) и касательных (25) напряжений, получим
(27)
где λ- константа Ламе, которая определяется по выражению:
(28)
Подставим выражение (28) в уравнение (27) и запишем,
(29)
где определяется по выражению (22), или в развернутом виде
Разделим выражение (29) на G и приведем подобные слагаемые и получим первое уравнение Ламе:
(30)
где - оператор Лапласа (гармонический оператор), который определятся как
(31)
Аналогично можно получить:
(32)
Уравнения (30) и (32) можно записать в следующем виде:
(33)
Уравнения (33) или (30) и (32) являются уравнениями Ламе. Если объемные силы равны нулю или постоянны, то
(34)
причем запись в данном случае не подразумевает суммирования по i. Здесь
(35)
или, с учетом (31)
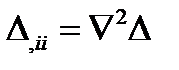(36)
Подставив (22) в (34) и проведя преобразования, получим
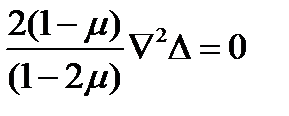
а, следовательно
(37)
где - функция, удовлетворяющая данному равенству. Если 
следовательно, f - функция гармоническая. Значит и объемная деформация также функция гармоническая.
Считая верным предыдущее предположение, возьмем гармонический оператор от i -ой строчки уравнения Ламе
(38)
где
(39)
Если объемные силы равны нулю или постоянны, то компоненты перемещения есть бигармонические функции.
Известны различные формы представления бигармонических функций через гармонические (удовлетворяющие уравнениям Ламе).
где k = 1,2,3. Причем
и 
Можно показать, что такое представление перемещений через гармоническую функцию обращает в тождество уравнения Ламе (33). Часто их называют условиями Попковича-Гродского. Четыре гармонические функции не обязательны, ведь ф0 можно приравнять нулю.