Главная | Обратная связь

Можно записать дифференциальное уравнение

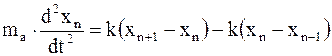; (17.85)

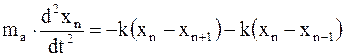; (17.86)

или

; (17.87)

Поскольку предполагается, что в кристалле в направлении цепочки распространяется звуковая волна, то воспользуемся выражением для смещения частиц (уравнением волны)

, (17.88)

где kx – запаздывание по фазе частиц, находящихся на расстоянии x от источника звука, по отношению к частицам, непосредственно граничащим с источником.

С точки зрения первый слева (n = 0) в цепочке атом (х = 0) имеет нулевое запаздывание по фазе, второй (n = 1) отстает от него по фазе на d, третий (n = 2) на 2d, … n-й на nd. Поэтому для смещения из равновесия n-го атома (молекулы) можно записать

. (17.89)

Сравнивая (17.88) и (17.89), получим

. (17.90)

Подставим выражение (17.89) в (17.89)

-m_аω²x₀cos(ωt-nδ) = kx_o{cos[(ωt-nδ)- δ]+

+cos[(ωt-nδ)+δ]-2cos(ωt-nδ)}. (17.91)

Воспользуемся тригонометрическим тождеством

cos(α+β)= cosα×cosβ-sinα×sinβ,

на основание которого получим

(17.92)

Длина звуковой волны λ значительно превосходит период кристаллической решетки d, тогда δ<<2p, так как разность фаз 2p набегает на расстоянии, равном длине волны. С учетом этого выражение (17.93) принимает вид

-m_aω² = k{2cosδ-2} или +m_aω²=2k{cosδ-1}. (17.93)

Воспользовавшись тригонометрическим тождеством

,

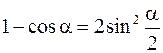преобразуем выражение (17.93)

.

Откуда следует

. (17.94)

Так как , то (17.94) преобразуется к виду

.

С другой стороны, скорость распространения волны v, частота колебаний n, длина волны λ связаны между собой соотношением , поэтому получаем

. (17.95)

Таким образом, скорость распространения звука в кристалле зависит от коэффициента квазиупругой силы k, который в свою очередь определяется жесткостью межмолекулярных связей, массы молекулы (атома), периода кристаллической решетки d. Чем сильнее возрастают силы межмолекулярного взаимодействия, при смещении молекулы из положения равновесия, тем больше параметр k и тем больше скорость звука. Наоборот, с утяжелением частиц усиливаются инертные свойства среды, а скорость звука согласно (17.95) становится меньше. Чем меньше d, тем более плотноупакованной является кристаллическая решетка, согласно (17.95) при этом скорость будет уменьшаться.

Не надо забывать, что выражение (17.95) для скорости звука в кристаллах получено для модели, которая, конечно, существенно отличается от реального объекта. Поэтому нельзя требовать от этого соотношения хорошего количественного согласия с опытом. Для нас важно, что соотношение (17.95) показывает большую роль, которую играют в распространении упругих волн молекулярные параметры, структура вещества.

В заключение отметим, что измерение скорости распространения звуковых волн в кристаллических твердых телах дает полезную информацию о кристаллическом состоянии, и что звуковые волны в кристаллах используются для реализации не разрушающегося метода контроля (дефектоскопии).

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основной

1. Савельев И.В. Курс общей физики. М.: Наука, 1989. Т. 1, 2, 3.

2. Трофимова Т.И. Курс физики. М.: Высшая школа, 1995. 472 с.

 

Дополнительный

1. Физика: Сборник контрольных заданий по механике для студентов инженерно-технических специальностей /Курск. гос. техн. ун-т. П.А. Красных, В.М. Пауков, В.М. Полунин, Г.Т. Сычёв; Под ред. В.М. Полунина. Курск, 1997. 93 с.

2. Физика: Сборник контрольных заданий по молекулярной физике и термодинамике для студентов технических специальностей /Курск. гос. техн. ун-т. В.Н. Бурмистров, П.А. Красных, В.М. Полунин, Г.Т. Сычев; Под ред. В.М. Полунина. Курск, 1997. 129 с.

3. Сивухин Д.В. Общий курс физики. М.: Наука, 1980. Т.1 - 6.

4. Сена Л.А. Единицы физических величин и их размерности. М.: Наука, 1977. 452 с.