 |
|
КРИВЫЕ ВТОРОГО ПОРЯДКА
Окружность.
Окружностью называется геометрическое место точек на плоскости, равноудаленных от некоторой точки, называемой центром.
Теорема. Если точка 
принадлежит окружности с центром в начале координат и радиуса r, то ее координаты удовлетворяют уравнению 
, и обратно.
Доказательство легко следует из теоремы Пифагора.ڤ
Уравнение называется каноническим уравнением окружности.
Эллипс.
Эллипсом называется геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние 2с между фокусами.
Теорема. Если точка принадлежит эллипсу с фокусами в точках 
и 
и сумма расстояний от нее до фокусов равна 2а, то ее координаты удовлетворяют уравнению 
, где 
, и обратно. (Уравнение называется каноническим уравнением эллипса.)
Доказательство. По определению эллипса имеем: 
. Перенося один радикал в правую часть, и возводя обе части уравнения в квадрат, получаем:
,
,
. Еще раз возводя обе части уравнения в квадрат, получаем: 
,
, 
. Учитывая, что , имеем: 
, то есть . Обратно, пусть точка удовлетворяет уравнению . Докажем, что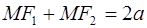 
. Действительно, 
= = 
=
= 
=
= 
=
= 
=
= 
=
= 
= 
=
= 
= 
=2а, поскольку 
и 
.ڤ
Эксцентриситетом эллипса называется отношение фокального расстояния к большой полуоси, то есть 
. Легко видеть, что 
.
Замечание. Если фокусы находятся на оси OY , то 
.
Гипербола.
Гиперболой называется геометрическое место точек на плоскости, для каждой из которых модуль разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2а, меньшее, чем расстояние 2с между фокусами.
Теорема. Если точка принадлежит гиперболе с фокусами в точках и и модуль разности расстояний от нее до фокусов равна 2а, то ее координаты удовлетворяют уравнению 
, где 
, и обратно. (Уравнение называется каноническим уравнением гиперболы.)
Доказательство. По определению гиперболы имеем:
. Тогда получается, что 
. Перенося один радикал в правую часть, и возводя обе части уравнения в квадрат, получаем:
,
,
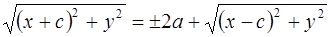. Еще раз возводя обе части уравнения в квадрат, получаем: ,
, . Учитывая, что , имеем: 
, то есть . Обратно, пусть точка удовлетворяет уравнению . Докажем, что 
. Действительно, 
= = 
=
= 
=
= 
=
= 
=
= 
=
= 
= 
=
= 
= 
.
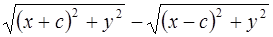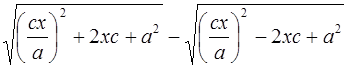То есть = 
2а. Следовательно . ڤ
Эксцентриситетом гиперболы называется отношение фокального расстояния к большой полуоси, то есть . Легко видеть, что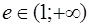 
.
Замечание. Если фокусы находятся на оси OY , то каноническое уравнение будет 
.
Теорема. Гипербола, уравнение которой , имеет асимптоты 
.
Доказательство. Покажем, что 
. Действительно, 
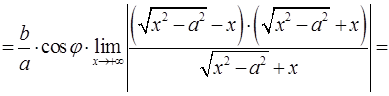
.ڤ
Парабола.
Параболой называется геометрическое место точек на плоскости, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус, и называемой директрисой.
Расстояние от фокуса параболы до ее директрисы называется параметром параболы.
Эксцентриситет параболы принимается равным единице.
Теорема. Если точка принадлежит параболе с фокусом в точке 
и директрисой 
, то ее координаты удовлетворяют уравнению 
, и обратно. (Уравнение называется каноническим уравнением параболы.)
Доказательство. По определению параболы имеем:
. Это уравнение эквивалентно следующему: 
. Раскрывая скобки, получаем: 
. Приводя подобные слагаемые, имеем: . Обратно, пусть точка удовлетворяет уравнению . Докажем, что расстояние от точки М до фокуса равно расстоянию от этой точки до директрисы. Действительно, расстояние от точки М до фокуса равно 
, то есть расстоянию от точки М до директрисы. ڤ
Замечание. Если фокус находятся на оси OY ( 
), а директриса имеет уравнение 
, то каноническое уравнение будет 
.