Главная | Обратная связь

Имитовставка по ГОСТ 28147-89

ГОСТ 28147-89 предусматривает выработку имитовставки в соответствующем режиме. Длина имитовставки от 1 до 32 бит. Её выработка происходит по следующей схеме.

Открытый текст разбивается на блоки длиной 64 бита. Последний блок в случае необходимости дополняется нулями.

Первый блок шифруется в режиме простой замены ГОСТ 28147-89 тем же ключом, что и сообщение, но с применением 16 циклов вместо 32. Результат по битам по модулю 2 складывается с вторым блоком и так же шифруется. Результат складывается с третьим блоком... и так далее.

Первые 32 бита получившегося блока составляют имитовставку. Спецификация шифра предусматривает использование в качестве имитовставки и меньшее количество бит по желанию, но не большее.

Имитовставка обычно передаётся в конце сообщения и может вычисляться либо отдельно от шифрования/расшифрования, либо в процессе оного.

[править]MAA

MAA (Message Authenticator Algorithm) — Алгоритм проверки подлинности сообщений.

Этот алгоритм является стандартом ISO. Он выдает 32-битовое хэш-значение и был спроектирован для мэйнфреймов с быстрыми инструкциями умножения.

v=v<<<1

e=v xor w

x=((((e+y) mod 2^32)۷A۸C)*(x xor Mi))mod 2^32-1

y=((((e+x) mod 2^32)۷B۸D)*(y xor Mi))mod 2^32-1

Эти действия повторяются для каждого блока сообщений, Mi, и результирующее хэш-значение получается с помощью XOR x и y. Переменные v и e зависят от ключа. A, B, C и D являются константами. Возможно, этот алгоритм широко используется, но он достаточно не безопасен. Он был разработан давным давно и не слишком сложный.

MAC

К MAC хэш-функциям для вычислений кодов аутентификации сообщений, подсемейству ключевых хэш-функций, относят семейство функций удовлетворяющих следующим свойствам:

· простота вычисления дайджеста от сообщения;

· сжатие данных — входное сообщение произвольной битовой длины преобразуется в дайджест фиксированной длины;

· стойкость ко взлому — имея одну и более пар сообщение-дайджест, (x[i], h(x[i])), вычислительно невозможно получить новую пару сообщение-дайджест (x, h(x)), для какого-либо нового сообщения x.

Если не выполняется последнее свойство, то MAC может быть подделан. Также последнее свойство подразумевает, что ключ невозможно вычислить, то есть, имея одну или более пар (x[i], h(x[i])) с ключом k, вычислительно невозможно получить этот ключ.

Алгоритмы получения кода аутентификации сообщения могут быть разделены на следующие группы по их типу:

· на блочных шифрах — например: CBC-MAC, RIPE-MAC1, RIPE-MAC3;

· получение MAC из MDC;

· кастомизированные алгоритмы — например: MAA, MD5-MAC;

· на потоковых шифрах — например: CRC-based MAC.

[править]Получение MAC на основе MDC

Существуют методы получения из MDC кодов аутентификации сообщений включением секретного ключа во входные данные алгоритма MDC. Недостатком такого подхода является то, что фактически на практике большинство алгоритмов MDC разработано так, что они являются либо OWHF, либо CRHF, требования к которым отличаются от требований к MAC алгоритмам.

1. secret prefix method : К последовательности блоков данных =x₁x₂x₃..x_n в начало приписывается секретный ключ k: k||x. Для данной последовательности данных с помощью итерационной хэш-функции вычисляется MDC, например, такой, что H₀=IV (от англ. initial value), H_i=f(H_i-1,x_i) h(x) = H_n. Таким образом, MAC =h(k||x). Минусом такого подхода является то, что третья сторона может дописать в конец последовательности блоков дополнительные данные y: k||x||y. Новый MAC может быть вычислен без знания ключа k: ₁ = f( ,y).

2. secret suffix method : Секретный ключ приписывается в конец последовательности данных: x||k. В этом случае MAC =h(x||k). В этом случае может быть применена атака методом дней рождений. При длине дайджеста в n бит. Третьей стороне понадобится порядка 2^n/2 операций, чтобы для сообщения x найти сообщение x’ такое, что h(x)= h(x’). При этом знание ключа k будет не обязательно. Узнав значение MAC для сообщения x, третья сторона сможет сгенерировать корректную пару (x’, ).

3. envelope method with padding : Для ключа k и MDC h вычисляется MAC от сообщения h_k(x)=(k||p||x||k), где p — строка, дополняющая ключ k до длины блока данных, для того, чтобы гарантировать, что будет произведено как минимум 2 итерации. Например, для MD5 k — 128 бит, а p — 384 бита.

4. HMAC : Для ключа k и MDC h вычисляется MAC от сообщения h_k(x)=(k||p₁||h(k||p₂||x)), где p₁,p₂ — различные строки, дополняющие k до длины блока данных. Такая конструкция довольно эффективна, несмотря на двойное использование h.

 

№ Линейные конгруэнтные генераторы. Регистры с обратной линейной связью. Линейная сложность. Корреляционная стойкость.

Линейный конгруэнтный метод — один из алгоритмов генерации псевдослучайных чисел. Применяется в простых случаях и не обладает криптографической стойкостью. Входит в стандартные библиотеки различных компиляторов.

Описание

Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

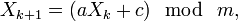
где a и c — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа и при разных его значениях получаются различные последовательности случайных чисел. В то же время, многие свойства этой последовательности определяются выбором коэффициентов в формуле и не зависят от выбора стартового числа.

[править]Свойства

Последовательность чисел, порождаемая линейным конгруэнтным методом, периодична с периодом, не превышающим m. При этом длина периода в точности равна mтогда и только тогда, когда:^[1]

1. НОД(c,m) = 1 (то есть, c и m взаимно просты);

2. a-1 кратно p для всех простых делителей p числа m;

3. a-1 кратно 4, если m кратно 4.

Статистические свойства получаемой последовательности случайных чисел полностью определяются выбором коэффициентов a и c. Для этих констант выписаны^[кем?]условия, гарантирующие удовлетворительное качество получаемых случайных чисел.

Генератор псевдослучайных чисел (ГПСЧ, англ. Pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).

Регистр сдвига с линейной обратной связью (РСЛОС, англ. Linear feedback shift register, LFSR) — регистр сдвига битовых слов, у которого входной (вдвигаемый) бит является линейной функцией состояния остальных битов регистра до сдвига. Может быть организован как программными, так и аппаратными средствами и применяется для генерации псевдослучайных последовательностей битов, что находит применение, в частности, в криптографии.

Определение

В регистре сдвига с линейной обратной связью выделяют две части (модуля): собственно регистра сдвига и схемы (или подпрограммы) вычисляющих значение вдвигаемого бита. Регистр состоит из функциональных ячеек (или битов машинного слова или нескольких слов), в каждой из которой хранится текущее состояние одногобита. Количество ячеек , называют длиной регистра. 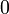Биты (ячейки) обычно нумеруются числами , каждая из которых способна хранить бит, причём в ячейку происходит вдвижение вычисленного бита, а из ячейки извлекается выдвигаемый очередной сгенерированный бит. Вычисление вдвигаемого бита обычно производится до сдвига регистра, и только после сдвига значение вычисленного бита помещается в ячейку .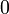

Периодом регистра сдвига называют минимальную длину получаемой последовательности до начала её повторения. Так как регистр из битовых ячеек имеет только разных ненулевых состояний, то, принципиально, период регистра не может превышать это число. Если период регистра равен этому числу, то такой регистр называют регистром максимального периода.

Для РСЛОС функция обратной связи является линейной булевой функцией от состояний всех или некоторых битов регистра. Например, сумма по модулю два или её логическая инверсия является линейной булевой функцией (операция XOR, в формулах обозначают как ) и наиболее часто применяется в таких регистрах.

При этом те биты, которые являются переменными функции обратной связи, принято называть отводами.

Управление регистром в аппаратных реализациях производится подачей сдвигающего импульса (иначе называемого тактового или синхроимпульса) на все ячейки, в программных — выполнением программного цикла, включающего вычисление функции обратной связи и сдвига битов в слове.

В течение каждого такта времени выполняются следующие операции:

· содержимое ячейки формирует очередной бит выходной последовательности битов;

· новое содержимое ячейки определяется битом обратной связи, являющегося значением функции обратной связи (обычно сложение по модулю ) с определёнными коэффициентами (принимающими значение 0 и 1) битов ячеек ;

· содержимое -й ячейки перемещается в ячейку для любого ;

· содержимое 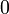-й ячейки принимает значение вычисленного бита.

Регистр сдвига с линейной обратной связью

Таким образом, в качестве функции обратной связи берётся логическая операция XOR (исключающее ИЛИ), то есть:

· на первом шаге:

· на втором шаге:

· …

· на -м шаге: , причём некоторые коэффициенты (но не все, иначе вырожденный случай) равны 0.

[править]Свойства примитивных многочленов

· если примитивный многочлен степени , то примитивен и ;

· если примитивен многочлен , то примитивен и ;

· если примитивен многочлен , то примитивен и .

[править]Свойства

Свойства выдаваемой РСЛОС последовательности тесно связаны со свойствами ассоциированного многочлена над полем . Его ненулевые коэффициенты называются отводами, как и соответствующие ячейки регистра, поставляющие значения аргументов функции обратной связи.

[править]Линейная сложность

Линейная сложность бинарной последовательности — одна из самых важных характеристик работы РСЛОС. Введём следующие обозначения:

· — бесконечная последовательность;

· — подпоследовательность длины 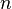последовательности ;

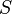· говорят, что РСЛОС генерирует последовательность 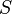, если существует некоторое исходное состояние, при котором выходная последовательность РСЛОС совпадает ;

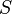· говорят, что РСЛОС генерирует конечную последовательность , если существует некоторое начальное состояние, для которого выходная последовательность РСЛОС имеет в качестве первых 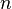членов члены последовательности .

Определение

Линейной сложностью бесконечной двоичной последовательности 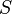называется число , которое определяется следующим образом:

· если — нулевая последовательность, то ;

· если не существует РСЛОС, который генерирует 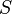, то ;

· иначе равна длине самого короткого РСЛОС, который генерирует .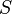

Линейной сложностью конечной двоичной последовательности называется число , которое равно длине самого короткого РСЛОС, который генерирует последовательность, имеющую в качестве первых 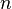членов .