 |
|
Поверхности второго порядка
Общее уравнение второй степени с тремя переменными
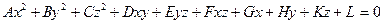
может определять в пространстве некоторую поверхность, называемую поверхностью второго порядка. С помощью преобразования системы координат уравнение такой поверхности может быть приведено к каноническому (простейшему) виду. Укажем различные типы поверхностей, описываемые каноническими уравнениями.
1. Сфера.
Множество точек пространства, равноудаленных от данной точки, называемой центром, называется сферой.
Уравнение сферы имеет вид
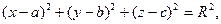
где С(a,b,c) – центр сферы, R- радиус сферы. Если центр сферы расположен в начале координат, то уравнение сферы принимает вид

2. Цилиндрические поверхности.
Цилиндрической поверхностью называется поверхность, составленная из всех прямых, пересекающих данную линию L и параллельных данной прямой l. При этом линия L называется направляющей цилиндрической поверхности, а каждая из прямых, составляющих эту поверхность и параллельных прямой l – образующей. Укажем уравнения цилиндрических поверхностей для случаев, когда направляющие лежат в одной из координатных плоскостей, а образующие параллельны координатной оси, перпендикулярной этой поверхности.
Уравнение вида F(x,y)=0 в пространстве определяет цилиндрическую поверхность с образующими, параллельными оси Оz. Аналогично, уравнение
F(x,z)=0 определяет цилиндрическую поверхность с образующими, параллельными оси Оy, и F(y,z) - цилиндрическую поверхность с образующими, параллельными оси Ох.
Канонические (простейшие) уравнения цилиндрических поверхностей второго порядка
 - эллиптический цилиндр;
- эллиптический цилиндр;
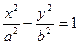 - гиперболический цилиндр;
- гиперболический цилиндр;
 - параболический цилиндр.
- параболический цилиндр.
Уравнения всех трех цилиндров с образующими, параллельными оси Оz, не содержат координаты z и совпадают с уравнениями направляющих, определяющих кривые второго порядка, соответственно эллипс, гиперболу и параболу, лежащих в плоскости Оху.
3. Конические поверхности.
Конической поверхностью называется поверхность, составленная всеми прямыми, пересекающими данную линию L и проходящими через данную точку Р. Линия L называется направляющей конической поверхности, точка Р – ее вершиной, а каждая из прямых, составляющих коническую поверхность, - образующей.
Пусть направляющей конической поверхности с вершиной в начале координат является эллипс

тогда можно получить уравнение конической поверхности в виде
 ,
,
которое называется конус второго порядка.
4. Эллипсоид.

а, b, c – полуоси эллипсоида.
5. Однополостной гиперболоид.

6. Двуполостной гиперболоид.

6. Эллиптический параболоид.

7. Гиперболический параболоид.

Литература: К.А. Хасеинов Каноны математики. Стр.110-120.