 |
|
Практическое занятие 7
1. Даны точки A(4;3;5), B(-3;2;1), C(2;-3;0). Найти координаты их проекций: а) на плоскость Оху; б) на плоскость Охz.
Отв.
а)A) 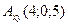 ,
, 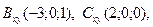 B)
B) 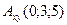 ,
, 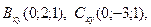
C) 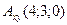 ,
, 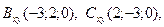 D)
D) 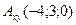 ,
, 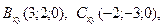
E) 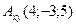 ,
, 
б) A) 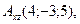 ,
, 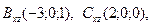 B)
B) 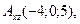 ,
, 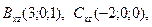
C) 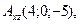 ,
, 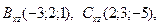 D)
D) 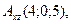 ,
, 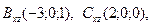
E)  ,
, 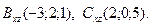
2. Вычислить расстояния от начала координат до точек А(4;-2;-4) и
В(-4;12;6).
Отв. A) ОА = 5, B) ОА = 7, C) ОА = 6,5, D) ОА = 6, E) ОА = 8,
A) OB =15. B) OB =13. C) OB =10. D) OB =12. E) OB =14.
3. Даны вершины треугольника 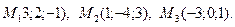 Найти середины его сторон.
Найти середины его сторон.
Отв. A) (2;0;-1), (-1;0;2), (0;0-2), B) (-2;-1;-1), (1;-2;2), (0;1;-2),
C) (2;1;-1), (-1;2;2), (0;-1;-2), D) (2;-1;1), (-1;2;2), (0;1;2),
D) (2;-1;-1), (-1;-2;2), (0;1;-2).
4. Даны две вершины А(2;-3;-5), В(-1;3;2) параллелограмма АВСD и точка пересечения его диагоналей (Е4;-1;7). Определить две другие вершины этого параллелограмма.
Отв. С(5;1;19) и D(9;-1;12).
5. Доказать, что треугольник с вершинами А(3;-1;2), В(0;-4;2) и С(-3;2;1) равнобедренный.
6. На оси абсцисс найти точку, расстояние которой от точки А(-3;4;8) равно 12.
Отв. A) (5;0;0) и (11;0;0), B) (-5;0;0) и (-11;0;0), C) (5;0;0) и (-11;0;0)
D) (4;0;0) и (-10;0;0), E) (4;0;0) и (-8;0;0).
7. На оси ординат найти точку, равноудаленную от точек А(1;-3;7) и В(5;7;-5).
Отв. A) (0;3;0) B) (0;4;0) C) (0;-2;0) D) (0;2;0) E) (0;-3;0
8. Составить уравнение плоскости, которая проходит через точку 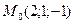 и имеет нормальный вектор
и имеет нормальный вектор 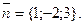
Отв. A) x-2y-3z+3=0. B) x-2y+3z-3=0. C) –x+2y+3z+3=0.
D) x+2y-3z-3=0. E) x-2y+3z+3=0.
9. Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор 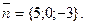
Отв. A) 5x-3z=0. B) 5x-y-3z=0. C) –5x+3z=0.
D) 5y-3z=0. E) 5x-3y=0.
10. Точка Р(2;-1;-1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости.
Отв. A) 2x-y-z+6=0. B)2x-y-z-6=0. C) 2x+y+z-6=0.
D) -2x-y-z+6=0. E) 2x+y-z+6=0.
11. Написать уравнение плоскости, проходящей через точку Р(2;2;-2) параллельно плоскости x-2y-3z+2=0.
Отв. A) x-2y-3z-2=0. B) –x+2y-3z+2=0. C) x-2y-3z-4=0.
D)2 x-2y-2z+2. E) x-2y+3z-4=0.
12. Найти угол между плоскостями 2x-2y+z-13=0 и x+z-6=0.
Отв. A)0. B) 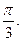 C)
C)  D)
D) 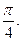 E)
E) 
13. Составить уравнение плоскости, которая проходит через точку 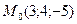 параллельно двум векторам
параллельно двум векторам 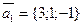 и
и 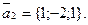
Отв. A) x-2y-3z+3=0. B) x-4y+7z-16=0. C) –x+4y+7z+13=0.
D) x+2y-3z+16=0. E) x+4y+7z+16=0.
14. Найти отрезки, отсекаемые плоскостью 3x-4y-6z+12=0 на координатных осях.
Отв. A) a=-4,b=3,c=2. B) a=4,b=3,c=2. C) a=3,b=4,c=6.
D) a=3,b=-4,c=-6. E) a=1/4,b=1/3,c=1/2.
15. Написать уравнение плоскости, проходящей через точку А(2;-1;1), перпендикулярно плоскостям 1) 2x-z+1=0 и y=0. 2) 2x-y+3z-1=0 и x+2y+z=0.
Отв. 1) х+2z-4=0. 2) –7x+y+5z+10=0.
16. Написать уравнение плоскости, проходящей через три точки А(1;-1;2), В(2;1;2) и С(1;1;4).
Отв. 2х-у+z-5=0.
17. Вычислить расстояние D от точки до плоскости в каждом из следующих случаев:
а) M(-2;-4;3), 2x-y+2z+3=0;
б) N(2;-1;-1) , 16x-12y+16z-4=0;
в) P(3;-6;7), 4x-3z-1=0.
Отв. а) A) 2, B) 1, C) 4, D) 3, E) 5.
б) A) 3, B) 2, C) 5, D) 4, E) 1,
в) A) 2. B) 3, C) 4, D) 1, E) 5.
18. Вычислить расстояние между параллельными плоскостями:
а) 4x-2y+4z-21=0, 2x-y+2z+9=0.
б) 16x+12y-15z+50=0, 16x+12y-15z+25=0
Отв. а) A) 5,5. .B) 12. C) 30. D)7. E) 6,5.
19. Найти угол между плоскостями x-2y+2z-8-0 и x+z-6=0.
Отв. A) 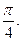 . B)
. B) 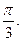 C)
C)  D)0. E)
D)0. E) 
20. Составить уравнения плоскостей, параллельных плоскости 2x-2y+z-3=0 и отстоящих от нее на расстоянии d=5.
Отв. 2x-2y+z+12=0, 2x-2y+z-18=0.
21. Составить уравнение плоскости, перпендикулярной к плоскости
2x-2y+z-3=0 и отсекающей на координатных осях Ох и Оу отрезки 
Отв. x-3y-2z+2=0.
22. Даны точки А(3;-1;2) и В(4;-2;-1). Составить уравнение плоскости, проходящей через точку А перпендикулярно вектору 
Отв. 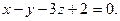
23. Составить канонические уравнения прямой, проходящей через точку 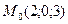 параллельно:
параллельно:
а) вектору 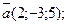
б) прямой  в) оси Ох; г) оси Оу; д) оси Оz.
в) оси Ох; г) оси Оу; д) оси Оz.
Отв.а) A)  B)
B) 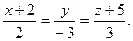 C)
C) 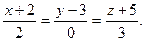 ,
,
D) 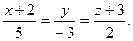 E)
E) 
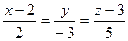 ,
,
б ) A)  B)
B) 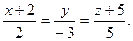 C)
C) 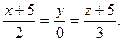 ,
,
D) 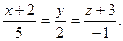 E)
E) 
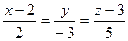 .
.
в) A)  B)
B) 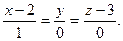 C)
C) 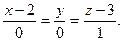
D) )  E) )
E) ) 
г) A)  B)
B)  C)
C) 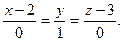
D)  E)
E) 
д) A)  B)
B) 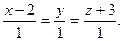 C)
C) 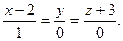
D) 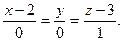 E)
E) 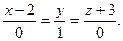
24. Составить канонические уравнения следующих прямых:
1)  2)
2) 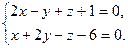
Отв. 1) 
25. Составить канонические уравнения прямой, проходящей через две данные точки: 1) (1;-2;1), (3;1;-1); 2) (3;-1;0), (1;0;-3); 3) (3;-2;1), (0;-2;3)..
Отв. 1)  2)
2) 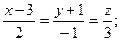 3)
3) 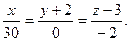
26. Написать канонические уравнения перпендикуляра, опущенного из точки А(2;-3;4) на ось Оz.
Отв. A) 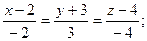 B)
B)  C)
C) 
D) 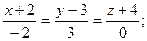 E)
E) 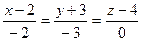
27. Найти острый угол между прямыми 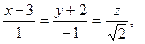
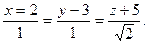
Отв. A) 30º ; B) 45º; C) 90º; D) 60º; E) 75º.
28. Найти тупой угол между прямыми 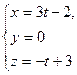 ,
, 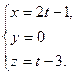
Отв. A) 130º ; B) 100º; C) 150º; D) 120º; E) 135º.
29. Найти угол между прямыми и плоскостями:
1) 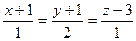 и
и 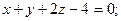 2)
2)  и
и 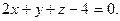
Отв. 1) 
30. Найти точку пересечения прямой и плоскости:
а) 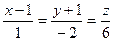 ,
, 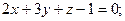
б) 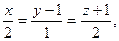

в) 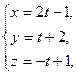
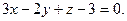
Отв. а) (2;-3;6), б) (6;4;5), в) (5;5;-2).
31. Составить уравнение плоскости, проходящей через прямую 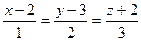 и точку (3;4;0).
и точку (3;4;0).
Отв. 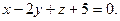
Литература:Линейная и векторная алгебра. Аналитическая геометрия. Сборник задач по высшей математике. Академия ГА Алматы 2010. Стр 57-61.