 |
|
Практическое занятие 8
⇐ ПредыдущаяСтр 4 из 4
Контрольная работа
По теме «Аналитическая геометрия в пространстве»
Варианты 1 –10
Вариант 1
Составить уравнение плоскости, проходящей через точку М(2;3;5) перпендикулярно вектору 
| A) 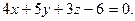 B) B)  C) C) 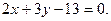 D) D)  E) E) 
| |
При каком значении m прямая  параллельна плоскости параллельна плоскости 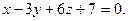
| A) m =1. B) m = 4 C) m = -3. D) m =-7. E) m =10. | |
Найти острый угол между прямыми

| A) 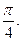 B) B)  C) C)  D) D) 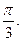 E) E) 
|
Вариант 2.
Составить уравнение плоскости, проходящей через точку М(3;4;-5) параллельно векторам 
| A)  B) B)  C) C)  D) D) 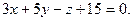 E) E) 
| |
Найти проекцию точки Р(2;-1;3) на прямую

| A) (5;6;7) B) (3;5;1) C) (1;2;5) D) (3;-2;4) E) (2;3;5). | |
Найти угол между прямой  и плоскостью и плоскостью 
| A) 120°. B) 135° C) 0° D) 90° E) 180°. |
Вариант 3.
Составить уравнение плоскости, которая проходит через точки 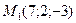 и и 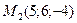 параллельно оси Ох. параллельно оси Ох.
| A)  B) B)  C) C)  D) D) 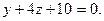 E) 4x-3y+z=0. E) 4x-3y+z=0.
| |
Найти проекцию точки Р(5;2;-1) на плоскость 
| A) (1;4;-7) B) (5;2;3) C) (1;0;4) D) (3;2;-7) E) (-4;5;-1). | |
Составить канонические уравнения прямой, проходящей через две данные точки 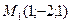 и и 
| A) 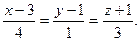 B) B)  C) C) 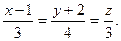 D) D) 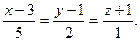 E) E) 
|
Вариант 4.
| Плоскость отсекает на осях равные отрезки, равные 3. Составить уравнение этой плоскости. | A) 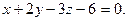 B) B)  C) C)  D) D) 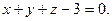 E) x+y+z=-4. E) x+y+z=-4.
| |
Найти точку пересечения прямой 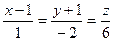 и плоскости и плоскости 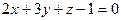 . .
| A) (4;3;1) B) (2;-3;6) C) (1;2;-3) D) (3;2;0) E) (6;1;-4). |
Найти расстояние между параллельными плоскостями: 
| A) 6. B) 4. C) 8. D) 12. E) 2.. |
Вариант 5.
Составить уравнение плоскости, проходящей через начало координат перпендикулярно к вектору 
| A)  B) B)  C) C) 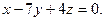 D) D)  E) E) 
| |||
Составить параметрические уравнения прямой, проходящей через две данные точки  и и 
| A)  В) В)  C) C)  D) D)  E) E) 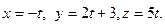
| |||
Составить уравнение плоскости, проходящей через прямую 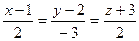 и точку А(2;-2;1). и точку А(2;-2;1).
| A) 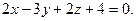 B) B)  C) C)  D) D)  E) E) 
| |||
Вариант 6.
| Составить уравнение плоскости, проходящей через ос Оz и точку А(3;-4;7). | A) 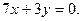 B) B) 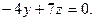 C) C)  D) D)  E) E) 
| |
Найти тупой угол между прямыми 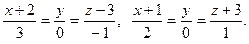
| A)  B) B) 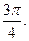 C) C) 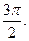 D) D)  E) E) 
| |
| Найти точку Q, симметричную точке P(1;3;-4) относительно плоскости 3х+у-2z=0. | A) (-5;1;0) B) (4;3;-2) C) (3;1;-4) D) (2;1;3) E) (0;4;3). |
Вариант 7.
Составить уравнение плоскости, проходящей через три данные точки 
| A)  B) B) 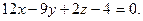 C) C)  D) D)  E) E) 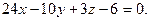
| |||
Составить параметрические уравнения прямой, проходящей через точку А(1;-1;-3) параллельно прямой 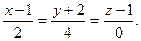
| A) 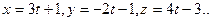 В) В)  C) C) 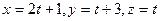 D) D)  E) E) 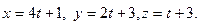
| |||
Найти точку пересечения прямой 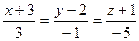 и плоскости и плоскости  . .
| A) (4;3;2) B) прямая параллельна плоскости. C) (1;2;-3) D) (-3;2;-1) E) (6;1;-4). | |||
Вариант 8.
| Найти отрезки, отсекаемые плоскостью 3х-4у-24z+12=0 на координатных осях. | A) а=3;b=0;c=4. B) a=5;b=1;c=0. C) a=-1;b=2;c=0. D) a=3;b=-2;c=0. E) a=6;b=1;c=-4.. | |
Найти точку пересечения прямой 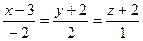 с координатной плоскостью Оху. с координатной плоскостью Оху.
| A) (3;0;4) B) (5;1;0) C) (-1;2;0) D) (3;-2;0) E) (3;1;-4). | |
Найти расстояние от точки М(2;3;-1) до прямой 
| A) 17. B) 30. C) 25. D) 21. E) 12. |
Вариант 9.
| Найти отрезки, отсекаемые плоскостью 2х-3у-4z-24=0 на координатных осях. | A) а=12;b=-8;c=-6. B) a=12;b=4;c=2. C) a=6;b=-4;c=8. D) a=10;b=3;c=4. E) a=-8;b=12;c=-6.. | |
| Даны вершины треугольника А(1;-2;-4), В(4;1;-3) и С(5;2;-6). Составить канонические уравнения его медианы, опущенной из вершины В на середину противоположной стороны. | A) 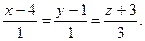 B) B) 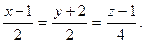 C) C)  D) D)  E) E) 
| |
Найти точку пересечения прямой  и плоскости и плоскости 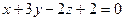 . .
| A) (3;5;2) B) (4;2;5) C) (3;6;1) D) (-4;4;5) E) (-2;3;2). |
Вариант 10.
| Составить уравнение плоскости, проходящей через ось Оу и точку М(1;4;-3). | A)  B) B) 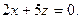 C) C) 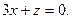 D) D)  E) E) 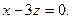
| |
| Вычислить расстояние между параллельными плоскостями 6x-18у-9z-28=0, 4x-12y-6z-7=0. | A) 2. B) 3,5. C) 6,5. D) 1. E) 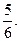
| |
Найти угол между прямыми 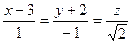 , ,

| A) 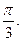 B) B) 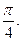 C) C) 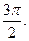 D) D)  E) E) 
|
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.