Главная | Обратная связь

Описание принципа работы заданной структурной электрической схемы устройства умножения двоичных чисел

Структурная электрическая схема устройства умножения четырехразрядных двоичных чисел представлена на рисунке 1.1.

 

Рисунок 1.1 – Устройство умножения двоичных чисел.

Схема электрическая структурная

 

Рассмотрим назначение узлов, входящих в структурную схему устройства.

Умножитель Y3 предназначен для умножения четырехразрядных двоичных чисел A и B, представленных разрядами , , , и 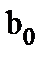, , , 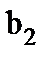. На выходе умножителя формируется восьмиразрядное произведение Q, представленное разрядами , ,…, .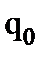

Регистр Y1 предназначен для параллельного ввода четырехразрядного множимого A в двоичной системе счисления (СС). Значение множимого A может меняться в пределах от 0 до 15 в десятичной СС.

Счетчик Y2 предназначен для параллельного ввода четырехразрядного множителя B в двоичной СС. Значение множителя B также может меняться от 0 до 15 в десятичной СС.

Регистр Y4 предназначен для параллельного вывода результата умножения, который представляет собой восьмиразрядное кодовое слово.

Загрузка сомножителей и запись результата умножения синхронизируется тактовыми импульсами 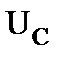. Причем ввод сомножителей осуществляется по отрицательным фронтам тактовых импульсов, а вывод результата умножения – по положительным.

Процесс функционирования устройства поясняется временной диаграммой, которая представлена на рисунке 1.2.

 

 

Рисунок 1.2 – Временная диаграмма, поясняющая процесс функционирования устройства умножения

 

В момент времени 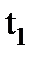по отрицательному фронту тактового импульса (рисунок 1.2) начинается ввод сомножителей в регистр Y1 и счетчик Y2 (рисунок 1.1). К моменту времени 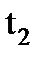ввод заканчивается, и начинается процесс умножения в умножителе Y3. Этот процесс в худшем случае завершается к моменту времени 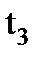. Затем по положительному фронту тактового импульса результат умножения записывается в регистр Y4 и т. д.

При подаче низкого уровня напряжения на вход (рисунок 1.1) устройство сбрасывается в исходное нулевое состояние.

Рассмотрим процесс умножения двоичных чисел на примере умножения заданных чисел[1]⁾, например: и . Умножение

выполним, начиная с младшего разряда множителя:

 

1 1 0 1

a3 a2 a1 a0

×

1 0 1 1

b3 b2 b1 b0

1 0 0 0 1 1 1 1

– множимое

1 1 0 1

1 1 0 1

0 0 0 0

+

1 1 0 1

+

+

q7 q6 q5 q4 q3 q2 q1 q0

– множитель

– частичные произведения

– полное произведение

 

Таким образом, при умножении двоичных чисел формируются частичные произведения, сдвигаются и суммируются.

Сравним результаты умножения чисел A и B в двоичной и десятичной СС. Для этого преобразуем результат умножения в десятичную систему счисления:

 

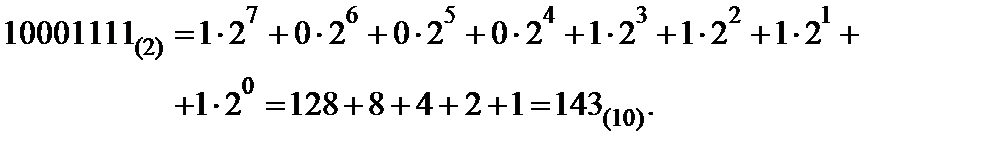
Они совпадают и равны .