Главная | Обратная связь

Построение их графиков.

НЕДЕЛЯ 8

Лекция 15

Исследование поведения функции и

построение их графиков.

Одной из важнейших прикладных задач дифференциального исчисления является разработка общих приемов исследования поведения функций.

Функция у=f(х)называется возрастающей (убывающей)в неко­тором интервале, если большему значению аргумента из этого интер­вала соответствует большее (меньшее) значение функции, т. Е. при x₁<x₂ выполняется неравенство

f(x₁)<f(x₂) (f(x₁)>f(x₂)).

Перечислим признаки возрастания (убывания) функции.

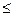1. Если дифференцируемая функция у=f(х) на oтрезке [а; b] воз­растает (убывает), то ее производная на этом отрезке неотрицательна (неположительна), т. Е. f'(х) 0(f' (х) 0).

2. Если непрерывная на отрезке [а; b] и дифференцируемая внутри него функция имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.

Функция y=f(х)называется неубывающей (невозрастающей)в некотором интервале, если для любых x₁<x₂ из этого интервала

f(x₁) 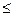f(x₂) (f(x₁) f(x₂)).

Интервалы, в которых функция не убывает или не возрастает, называются интервалами монотонности функций, Характер монотон­ности функции может изменяться только в тех точках ее области опре­деления, в которых меняется знак первой производной. Точки, в которых первая производная функции обращается в нуль или терпит разрыв, называются критическими.

Точка x₁называется точкой локального максимума функции у=f(x), если для любых достаточно малых | | 0 выполняется нера­венство f(x₁+ )<f(x₁). Точка x₂называется точкой локального ми­нимума функции у=f(х), если для любых достаточно малых | | 0 справедливо неравенство f(x₂+ )>f(х₂). Точки максимума и мини­мума называют точками экстремума функции, а максимумы и минимумы функции – ее экстремальными значениями.

Теорема 1 (необходимый признак локального экстремума). Еслифункция. У=f(х) имеет в точке х=х₀ экстремум, то либо f'(х₀)=0, либо f'(х₀) не существует.

В точках экстремума дифференцируемой функции касательная к ее графику параллельна оси Ох.

Теорема 2 (первый достаточный признак локального экстремума). Пусть функция у=f(х) непрерывна в некотором интервале, содержа­щем критическую точку х=х₀ и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки х₀). Если f'(х) при х<х₀ положительна, а при х>х₀ отрицательна, то при х=х₀ функ­ция у=f(х) имеет максимум. Если же f '(х) при х<х₀ отрицательна, а при х>х₀ положительна, то при х=х₀ данная функция имеет минимум.

Следует иметь в виду, что указанные неравенства должны выпол­няться в достаточно малoй окрестности критической точки х=х₀. Схема исследования функции у=f(х) на экстремум с помощью первой произ­водной может быть записана в виде таблицы.

Теорема 3 (второй достаточный признак локального экстремума функции).Пусть функция у=f(х) дважды дифференцируема и f'(х₀)=0. Тогда в точке х=х₀ функция имеет локальный максимум, если f»(х₀)<0, и локальный минимум, если f «( х₀)>0.

В случае, когда f»(х₀)=0, точка х= х₀ может и не быть экстремальной..

Кривая, заданная функцией y=f(х), называется выпуклойв ин­тервале (а; b),если все точки кривой лежат не выше любой ее касатель­ной в этом интервале, и вогнутойв интервале (а; b), если все ее точки лежат не ниже любой ее касательной в этом интервале.

Точка кривой М (х₀, f(х₀))отделяющая выпуклую ее часть от вогну­той, называется точкой перегиба кривой. Предполагается, что в точке М существует касательная.

Теорема 4 (достаточное условие выпуклости (вогнутости) графика функции).Если во всех точках интервала (а;b) вторая производная функции у=f(x) отрицательна (положительна), т. Е. f»(х)<0 (f»(x)>0), то кривая у=f(x) в этом интервале выпукла (вогнута).

В точке перегиба, отделяющей промежуток выпуклости от про­межутка вогнутости, вторая производная функции изменяет свой знак, поэтому в таких точках вторая производная функции или обращается в нуль, или не существует.

Теорема 5 (достаточный признак точки перегиба).Если в точке х = х₀ f»(х₀)=0 или f»(х₀) не существует и при переходе через эту точку производная f»(х) меняет знак, то точка с абсциссой х=х₀, кривой у=f(x) – точка перегиба.

Прямая L называется асимптотойданной кривой у=f(x), если расстояние от точки М кривой до прямой L при удалении точки М в беско­нечность стремится к нулю. Из определения следует, что асимптоты
могут существовать только у кривых, имеющих сколь угодно далекие точки («неограниченные» кривые).

Если существуют числа х=x_i (i=1,…,n), при которых т.е. функция имеет бесконечные разрывы, то прямые х=x_i называются вертикальными асимптотами кривой у=f(х). Если существуют пределы

то прямая у=kх+b называется наклонной асимптотой кривой у=f(х)(при k=0 – горизонтальной). При х можем прийти к двум значе­ниям для k. Если имеем одно значение для k, то при х можем получить два значения для b.

Для полного исследования функции и построения ее графика можно рекомендовать следующую примерную схему:

1) указать область определения функции;

2) найти точки разрыва функции, точки пересечения ее графика с осями координат и вертикальные асимптоты (если они существуют);

3) установить наличие или отсутствие четности, нечетности, периодичности функции;

4) исследовать функцию на монотонность и экстремум;

5) определить интервалы выпуклости и вогнутости, точки перегиба;

6) найти асимптоты графика функции;

7) произвести необходимые дополнительные вычисления;

8) построить график функции.

 

Литература: К.А. Хасеинов Каноны математики. Стр.190-201

 

 

Лекция 16