 |
|
Практическое занятие 16
Пример.Исследовать функцию  и построить ее график.
и построить ее график.
Решение.1) Функция определена при х > 0. (0,+¥) – область определения.
2). Исследуем поведение функции на границе области определения.
3) Из предыдущего пункта следует, что прямая х = 0 является вертикальной асимптотой, а прямая у = 0 – горизонтальной асимптотой. Будем находить невертикальные асимптоты y = kx +b.
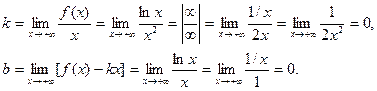
Так как 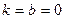 , то наклонной асимптоты нет; прямая у = 0 – горизонтальная асимптота.
, то наклонной асимптоты нет; прямая у = 0 – горизонтальная асимптота.
4) Найдем точку пересечения c осью Ох. Если у = 0, то  Точка Р(1;0) есть точка пересечения графика функции с осью Ох.
Точка Р(1;0) есть точка пересечения графика функции с осью Ох.
5) Функция  будет функцией общего вида, так как область определения функции не является симметричной относительно начала координат, и поэтому не выполняются условия четности и нечетности функции. Функция непериодическая.
будет функцией общего вида, так как область определения функции не является симметричной относительно начала координат, и поэтому не выполняются условия четности и нечетности функции. Функция непериодическая.
6) Для нахождения интервалов монотонности и экстремумов функции найдем критические точки. Для этого найдем первую производную 
Решив уравнение  найдем критические точки, подозрительные на экстремум.
найдем критические точки, подозрительные на экстремум. 
 - критическая точка.
- критическая точка.
Исследуем знак первой производной при переходе через критическую точку в сторону возрастания х. Результаты исследования представим в виде таблицы.
| х | (0,e) | e | (e,¥) |
| y’ | + | - | |
  у у
| возрастает | max | убывает |
 ,
, 

 - интервал возрастания,
- интервал возрастания,  интервал убывания.
интервал убывания.
6) Для нахождения интервалов выпуклости и вогнутости и исследования на перегиб найдем вторую производную. 
Решив уравнение  найдем критические точки второго рода.
найдем критические точки второго рода.
 критическая точка второго рода.
критическая точка второго рода.
Исследуем знак второй производной при переходе через критическую точку в сторону возрастания х. Результаты исследования представим в виде таблицы.
| х | (0,  ) )
| 
| 
|
| y” | 
| 
| |
| y | выпуклый | Пере-гиб | вогнутый |

 точка перегиба графика функции.
точка перегиба графика функции.

 8) Используя результаты исследования, строим график функции
8) Используя результаты исследования, строим график функции

 у
у






O 1 e  x
x
Упражнения.
Исследовать функцию и построить ее график.
1.  2.
2. 
3.  . 4.
. 4. 
5.  . 6.
. 6. 
7. 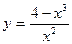 . 8.
. 8. 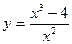 .
.
9.  . 10.
. 10. 
11.  . 12.
. 12.  .
.
13.  . 14.
. 14.  .
.
15. 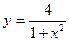 . 16.
. 16. 