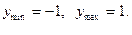 |
|
Возрастание и убывание функции. Экстремум функции
Функция y= f(x) называется возрастающей (убывающей) на (a,b), если для любых 
, таких, что 
( 
).
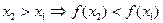Возрастающие и убывающие функции называются монотонными.
Достаточные признаки монотонности функции.
Если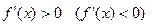 
" 
на (а,b).
Точка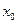 
называется точкой максимума (минимума) функции y= f(x), если функция непрерывна в этой точке и можно указать такую d-окрестность точки 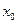, что для всех х 
, принадлежащих этой окрестности, выполняется неравенство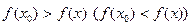 
При этом значение 
называется максимумом (max) (минимумом (min)) функции. Максимум и минимум функции называются экстремумом.
Необходимое условие существования экстремума. Если в точке 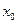функция непрерывна и имеет экстремум, то f’( 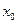) = 0 или производная в этой точке не существует.
Точки, в которых производная равна нулю или не существует, называются критическими точками первого рода.
Достаточный признак существования экстремума.
Пусть функция y=f(x) определена и непрерывна в некоторой окрестности точки 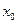, включая саму точку, и производная f’( 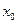) существует в окрестности этой точки, за исключением, быть может, самой точки .
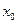Тогда, если:
1) 
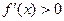(знак +) при х< 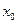и 
(знак -) при х> 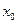, то функция в точке 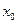достигает максимума;
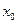2) (знак - ) при х< и 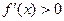(знак +) при х> 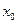, то функция в точке 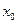достигает минимума;
3) f’( 
) не меняет знак, то экстремума нет.
Пример. Найти интервалы монотонности и экстремумы функции 
Решение.Область определения – вся числовая ось. D(f) = (-¥,¥)
Находим производную f’(x). 
= 
Решая уравнение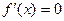 
, находим критические точки первого рода, т.е. точки, в которых производная либо равна нулю, либо не существует.
критические точки первого рода.
| х | (-¥,-1) | -1 | (-1,1) | (1,¥) | |
| y’ | - | + | - | ||
   y
| min | max |
Интервалы (-¥,-1), (1,¥) – интервалы убывания. Интервал (-1,1) – интервал возрастания. В точке х = -1 функция имеет минимум, в точке х = 1 – максимум. 
