 |
|
Достаточное условие выпуклости и вогнутости функции
Если f”(x)<0 для xÎ (a,b), то функция выпукла на интервале (a,b), а если f”(x)>0 для xÎ (a,b), то функция вогнута на этом интервале.
Точка графика функции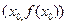 
, отделяющая выпуклую часть графика функции от вогнутой, называется точкой перегиба.
Необходимое условие существования точки перегиба
Если непрерывная функция y= f(x) имеет в точке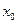 
перегиб, то 
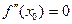или вторая производная в этой точке не существует.
Точки, в которых 
или вторая производная в этих точках не существует, называются критическими точками второго рода.
Достаточные условия существования точки перегиба.
Если при переходе через критическую точку слева направо вторая производная меняет знак, то имеется перегиб; если перемены знака нет, то перегиба нет.
Пример. Найти интервалы выпуклости, вогнутости и точки перегиба функции y= 
.
Решение.Найдем область определения функции. D(f) =(-¥,+¥)
Найдем вторую производную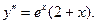 
Найдем критические точки второго рода. 
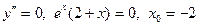- критическая точка.
| х | (-¥,-2) | -2 | (-2,+¥) |
| y” | - | + | |
| y | выпукла | Пер. | вогнута |
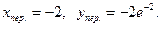(-2, -2 
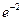) – точка перегиба.
(-¥,-2) - интервал выпуклости, (-2,+¥) - интервал вогнутости.
Асимптоты графика функции.
При исследовании функции необходимо установить ее поведение при удалении текущей точки графика функции от начала координат. В некоторых случаях это можно сделать с помощью прямой, к которой неограниченно приближается текущая точка графика функции при удалении ее от начала координат.
Асимптотой графика функции y = f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении ее от начала координат.
Различают вертикальные, горизонтальные и наклонные асимптоты. Пусть М(х,у) – текущая точка графика функции. Точка М (х,у) может удаляться от начала координат следующим образом:
1) х® а, у® ¥; 2) х®¥, у® b, 3) x®¥, y®¥.
В первом случае имеем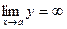 
, и прямая x = a является вертикальной асимптотой.
Во втором случае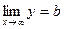 
и прямая y = b будет горизонтальной асимптотой.
В третьем случае график функции y = f(x) имеет наклонную асимптоту, уравнение которой имеет вид y = kx +b.
Необходимое и достаточное условие существование невертикальных асимптот устанавливается с помощью теоремы:
Теорема. Для того чтобы прямая y = kx +b была асимптотой графика функции 
, необходимо и достаточно существование пределов
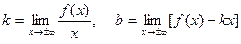
Если не существует хотя бы один из пределов, то невертикальных асимптот нет.
Пример. Найти асимптоты графика функции 
Решение. Точки х = 1 и х = -1 являются точками разрыва второго рода данной функции. Так как 
и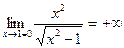 
, то прямые 
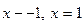являются вертикальными асимптотами.
Найдем невертикальные асимптоты. При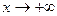 
получаем
, 
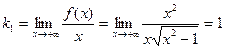Следовательно, правой асимптотой является прямая у = х.
Аналогично, при 
имеем.
, 
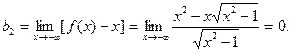
Левой асимптотой графика функции является прямая у = -х
Литература: К.А. Хасеинов Каноны математики. Стр.204-209