Неадекватность принимаемых моделей реальным объектам.

Стр 1 из 6Следующая ⇒

Источники и оценка методических погрешностей измерений

Методические погрешности обусловлены:

1) неопределенностью (дисперсностью) объекта измерений;

2) неадекватностью принимаемых моделей реальным объектам;

3) несовершенством методов измерений;

4) упрощением зависимостей, положенных в основу измерений;

5) неправильным использованием средств измерений;

6) разницей между значениями измеряемой величины на входе средства измерений и в точке отбора;

7) взаимодействием средства измерений и объекта измерений;

8) влиянием внешних условий.

Основной отличительной особенностью методических погрешностей является то обстоятельство, что они не могут быть указаны в технической документации на средства измерений, а должны оцениваться самим экспериментатором при разработке (аттестации) измерительной технологии (методики выполнения измерений).

Рассмотрим основные источники и способы оценки методических погрешностей измерений.

1. Неопределенность (дисперсность) объекта измерений.

Недостаточное знание реального объекта может быть первым источником искажения результата измерения, так как не позволяет точно сформулировать понятие измеряемой величины.

Например, под длиной предмета понимают расстояние между двумя выбранными точками на обоих его концах. Но при каждом значении температуры Т>0 К атомы в этих точках совершают температурные колебания, так что расстояние между ними меняется. Электронная оболочка окружает ядро как облако, причем вероятность нахождения электронов в определенной точке пространства по мере удаления от ядра постоянно уменьшается.

Высоту земной атмосферы невозможно указать, потому что воздушная оболочка бесконечно простирается в мировом пространстве. Резкой границы, до которой простирается воздушная оболочка, не существует. Чтобы все-таки решить поставленную задачу, необходимо уточнить предварительно ее постановку, определив, что следует понимать под высотой земной атмосферы. Например, ее граница может быть задана из условия, что там давление воздуха должно составлять 1% давления на уровне моря. Но возможны также и другие условия определения границы.

Неадекватность принимаемых моделей реальным объектам.

При установлении цели измерений – определение уровня интересующего нас свойства объекта (совокупности свойств) – и формализации измерительной задачи используется математическая модель объекта измерений, параметры которой являются величинами, подлежащими измерению. Выбранная модель должна удовлетворять следующим требованиям:

1) соответствие модели реальному объекту. Адекватность модели проверяется экспериментально. При этом погрешность несоответствия модели реальному объекту не должна превышать 10% от заданного предела погрешности измерения. Максимальная разность результатов измерений (размах) параметра обычно принимается в качестве числовой характеристики погрешности модели;

2) нестабильность измеряемых параметров модели объекта в течение времени измерения не должна превышать 10% от заданного предела погрешности измерений. Строго говоря, измерять можно только постоянные физические величины. Когда речь идет об измерении переменной физической величины, то под этим понимают либо измерение постоянных параметров этой величины, либо ее измерение в отдельные моменты времени. Например, напряжение переменного тока U(t) изменяется в зависимости от времени t по закону

где А – амплитуда напряжения переменного тока; w - угловая частота; j - начальная фаза.

Амплитуда А, угловая частота w и начальная фаза j, являющиеся параметрами напряжения, могут быть измерены. Может быть измерено также напряжение U₁,…,U_n в моменты времени t₁,…,t_n ;

3) компактность модели, обеспечивающая удобство ее последующего использования. Обеспечить компактность модели – это значит не вводить в нее лишних членов, ни тем более лишних факторов. Но это требование входит в противоречие с требованием наибольшей точности описания исследуемого явления. Отбор для включения в модель только тех факторов и тех дополнительных членов, которые действительно повышают точность описания исследуемого явления, может быть осуществлен лишь на основе использования соответствующих методов.

Выбор модели определяется реальными свойствами объекта измерений и целью измерений. Например, при измерении радиуса (диаметра) диска в качестве модели может использоваться круг, представляющий собой геометрическое место точек, равноудаленных от центра.

Рис. 5.1.

Уравнение круга в полярных координатах

Радиус круга – это параметр модели, соответствующий измеряемой физической величине (радиусу диска при одноконтактной схеме измерения).

Принятая модель не всегда учитывает все свойства реального объекта по причине их неизвестности или упрощения модели. Вследствие этого возникает составляющая погрешности измерений, обусловленная неадекватностью принятой модели объекта измерений реальному объекту или кратко - погрешностью от неадекватности моделирования объекта измерений. Она может быть определена как разность

где x_ист – истинное значение измеряемой величины x (параметра модели); С_ист – истинное значение количественной меры С определяемого свойства реального объекта измерений.

Несоответствие модели реальному объекту может быть оценено на основе предварительных измерений и анализа объекта измерений. Например, в случае с диском назначение диска позволяет определить допускаемую погрешность измерений и выбрать соответствующее средство измерений.

При выборе технологии измерений следует учитывать, что радиус круга инвариантен к направлению измерения (углу j), а радиус диска может быть разным при разным углах j. Поэтому измерение радиуса диска нужно выполнить в нескольких разных направлениях, чтобы проверить, насколько объект измерения и его математическая модель соответствует друг другу. Если разности результатов измерений радиусов будут незначительными (например, меньше возможной погрешности измерений), то в качестве результата измерения можно взять любой из полученных результатов наблюдений. Найдя значение измеряемой величины – именованное число, мы определим оценку истинного значения измеряемой величины (радиуса диска). Если разность результатов измерений радиусов диска в разных направлениях существенна (например, превышает уровень погрешности данного измерения), то приходится констатировать, что при требуемой точности измерений у диска нет одного радиуса, как у круга. Следовательно, выбранная модель не соответствует свойствам реального объекта и поставленную измерительную задачу нельзя решить. Таким образом, если в результате измерения нельзя получить какое-то именованное число – оценку истинного значения измеряемой величины, то измерение невозможно.

Если целью измерений является определение не радиуса диска, а отклонения от круглости, то в данном случае в качестве математической модели диска используется некоторая функция, выражающая зависимость радиуса от угла j

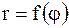
или для отклонения от круглости

где r₀ – радиус прилегающей окружности.

Рис. 5.2

Когда целью измерений является определение радиуса диска, в действительности его диаметр может быть разным в разных направлениях. Но пока это непостоянство было пренебрежимо мало, мы могли считать, что круг как модель соответствует объекту, и, следовательно, существует какое-то постоянное, фиксированное истинное значение измеряемой величины, а в результате измерения можно найти его оценку. Когда измерение выполнено, мы можем считать, что истинное значение измеряемой величины лежит где-то вблизи полученной оценки и отличается от нее не больше, чем на погрешность измерений.

Таким образом, идеализация, необходимая для построения модели, обусловливает неизбежное несоответствие между параметром модели и реальным свойством объекта. Это несоответствие называется пороговым несоответствием и является одним из источников методической погрешности измерений. Если методическая погрешность измерений, обусловленная пороговым несоответствием модели и объекта, превышает предел погрешности измерений, то измерение с требуемой точностью становится невозможным. Это свидетельствует о непригодности модели. Для продолжения эксперимента надо снизить, если возможно, требования к точности измерений или переопределить модель. Так, в случае измерения радиуса диска такой другой моделью мог бы быть круг, описывающий диск.

Для оценки адекватности модели и объекта измерений можно использовать дисперсионный анализ. Для этого проводят многократные измерения исследуемого параметра в разных точках объекта измерений. Например, измерение радиуса диска производят в разных направлениях.

Рис.5.3

Непостоянство результатов измерения x_i зависит от нескольких факторов: дисперсности объекта измерений, обусловленной отклонениями формы исследуемого объекта (например, отклонением от круглости диска) и дисперсности измерений, обусловленной случайным характером погрешности измерений. С помощью дисперсионного анализа можно установить степень влияния каждого из факторов на результаты измерения параметров объекта.

С этой целью в каждой точке исследуемого объекта производят многократные измерения исследуемого параметра. Пусть число точек (групп наблюдений) будет m и число наблюдений в каждой точке равно n. Всего мы располагаем mn измерениями, которые обозначим через x_ij, где i – номер точки, а j – номер произведенного в этой точке наблюдения, так что i изменяется от 1 до m, а j – от 1 до n. Таблица результатов измерений имеет следующий вид:

Таблица 5.3

Номер	Результаты измерений
точки	Номер наблюдения
объекта			…	n
	x₁₁	x₁₂		x_1n
	x₂₁	x₂₂		x_2n
M	M	M	M	M
m	x_m1	x_m2		x_mn

Общая дисперсия S² всех результатов измерения x_ij характеризует их рассеивание вследствие действия всех факторов и потому является суммарной дисперсией. Для выявления влияния отдельных факторов общую дисперсию разбивают на составляющие 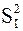и , характеризующие дисперсность объекта (несоответствие модели) и дисперсность измерений (случайный характер погрешности измерений).

Рассматривая составляющие суммарной дисперсии, т.е. производя дисперсионный анализ, можно решить вопрос о существенности влияния факторов на результат измерений.

Для этого вычисляют среднее арифметическое значение из ряда наблюдений в каждой точке

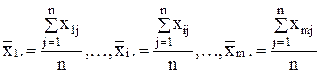
и общее среднее арифметическое значение всех mn наблюдений

Нас интересует, является ли расхождение между средними арифметическими значениями в каждой группе (точке) 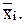случайным (обусловленным ограниченным числом неточных измерений) или же оно отражает влияние систематических факторов (неадекватность модели), т.е. мы хотим проверить нулевую гипотезу о допустимости расхождения средних арифметических Н₀: 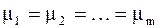. Для этого вычислим критерий

где 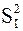- межгрупповая дисперсия (имеет число степеней свободы k₁=m-1);

- средняя дисперсия групп (имеет число степеней свободы k₂=m(n-1));

- сумма квадратов отклонений между группами;

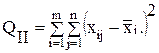- сумма квадратов отклонений внутри групп.

представляет собой сумму квадратов разностей между средними 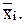отдельных групп (точек объекта измерений) и общей средней по всей совокупности наблюдений. Она характеризует степень расхождения между группами (точками объекта измерений), т.е. дисперсность объекта.

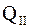представляет сумму квадратов разностей между отдельными наблюдениями и средней соответствующей группы. Она характеризует «остаточное рассеивание» случайных погрешностей измерений.

«Общая» или «полная» сумма квадратов отклонений отдельных наблюдений от общей средней

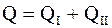где .

Оценки дисперси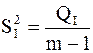й и имеют

c²-распределение с числом степеней свободы k₁=m-1 и k₂=m(n-1).

Критерий следует F-распределению Фишера с k₁=(m-1) и k₂=m (n-1) степенями свободы. Различие средних арифметических считают допустимым, если F при выбранном уровне значимости q лежит в пределах и

В этом случае следует сделать вывод об адекватности модели и объекта измерений.

Если значение F находится вне интервала 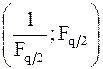, это означает, что между средними арифметическими групп (точками объекта измерений) имеются недопустимые смещения, которые не могут быть объяснены за счет действия случайных факторов.

Поэтому нулевая гипотеза Н₀: должна быть отброшена. Это означает, что исследуемый параметр модели (например, радиус круга) не является постоянным. Таким образом, следует сделать вывод о несоответствии модели объекту измерений.

За оценку методической погрешности измерений, обусловленной несоответствием модели объекту измерений, может быть принято среднее

квадратическое отклонение /Ön (точечная оценка) или доверительный интервал (интервальная оценка), границы которого определяются по формуле

где t – коэффициент Стьюдента, зависящий от доверительной вероятности Р=(1-q) и числа степеней свободы k₁=(m-1).

Пример 5.6. Для измерения диаметра диска (рис. 5.4,а) выбрана модель – круг с постоянным радиусом r=r₀=const.

r_i

а) б)

Рис. 5.4

Для проверки адекватности модели и объекта измерений проводятся многократные измерения (n=5) радиуса диска r_i в трех точках (m=3) (рис. 5.4, б). Измерения проводятся на вертикальном оптиметре методом сравнения. Результаты наблюдений представлены в табл. 5.4.

Таблица 5.4

Номер точки объекта	Результаты наблюдений, мкм
r_i1	r_i2	r_i3	r_i4	r_i5
	-7	-3	-5	-7	-3
	-5	-5	-3	-1	-1
	-3	-3	+1	+1	-1

Оценить адекватность модели и объекта измерений.

Решение. Для оценки адекватности модели и объекта измерений используем дисперсионный анализ.

По результатам наблюдений вычислим средние арифметические значения 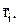, из пяти наблюдений в каждой точке объекта и их средние квадратические отклонения. Результаты расчетов представим в виде табл. 5.5:

Таблица 5.5

Номер точки объекта	Результаты наблюдений, мкм	, мкм	мкм²	мкм²
r_i1	r_i2	r_i3	r_i4	r_i5
	-7	-3	-5	-7	-3	-5
	-5	-5	-3	-1	-1	-3
	-3	-3	+1	+1	-1	-1

12 3 4 5 6 Следующая ⇒