Главная | Обратная связь

Проблема невизначеності та випадковості

У широкому розумінні випадковість може ототожнюватись з невизначеністю і у вужчому розумінні як від невизначеності, що підпорядковується певній закономірності та спричинена розподілом ймовірностей.

На підставі такого розподілу можна робити цілком обґрунтовані висновки щодо поведінки об’єкта, щодо його різних усереднених характеристик. Надалі імовірність трактуватимемо тільки у вузькому, імовірнісному сенсі, а в інших випадках вживатимемо термін невизначеність. Пояснимо різницю між випадковістю і невизначеністю детальніше.

При описі зв’язків між деяким комплексом умов S та події A, щодо якої за цих умов можна точно встановити, чи відбулася вона, чи ні, зазвичай використовують одну з двох схем:

1) за кожного виконання умов S подія A відбувається (тоді говорять про детермінований, однозначний зв’язок між умовами S та подією A);

2) за виконання умов S неможливо точно передбачити, чи відбудеться подія A, (іноді вона відбувається, іноді ні; тоді говорять про невизначеність події).

Над подіями можна виконувати певні операції. Об’єднанням (перерізом) подій A і B називають подію A B (A B) , за якої відбувається принаймні одна з подій А чи В (відбуваються одночасно обидві події А та В).

Подію , яка полягає в тому, що подія A не відбулася, називають протилежною до події A .

Подію A називають різницею A/B подій A і B (полягає в

тому, що відбувається подія A і не відбувається подія B ).

Подію , яка завжди відбувається за умов S, називають вірогідною (наприклад, ), подію ø , яка ніколи не відбувається за умов S, називають неможливою (наприклад, ).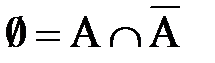

Множина подій F, які можуть відбуватися при комплексі умов S з введеними операціями, утворює так звану алгебру подій.

Щодо ймовірнісно випадкових подій, то вважають, що можна виконувати велику кількість експериментів, спостерігаючи за їхнім виникненням при незмінному комплексі умов S. Частоти виникнення кожної такої події в серії з n повторень експериментів обчислюють за формулою:

, (2.9) де – число експериментів в серії, коли А відбувається, за великих значень n групуватимуться коло певного числа Р(А). Це число ще називають імовірністю виникнення випадкової події А, воно є мірою можливості виникнення події А у зазначеному вище розумінні. А експеримент називають імовірнісним або стохастичним. Ймовірнісно випадкові події повинні володіти властивістю групування їхніх частот навколо їхніх ймовірностей.

Чимало невизначених подій мають подібну властивість, і, отже, можуть бути об’єктом вивчення теорії ймовірностей. Наприклад, це події, які відбуваються в азартних іграх, події спадкування тих чи інших ознак у живих істот.

Однак існують і невизначені події, що не є ймовірнісно випадковими. Наприклад, така: завтра у цій місцевості 56(враховуючи спостереження з метеорологічною ситуацією за багато років) о 12 год. очікують опадів граду (снігу, дощу), оскільки тут неможливо за даними метеорологічних досліджень утворити частоти цих подій.

З означення частоти (2.9) випливають такі властивості:

1) , ;

2) для будь-якої події А;

3) якщо (тобто події несумісні), то

Для ймовірнісно випадкових подій (оскільки за великих n їхні частоти групуються навколо ймовірностей подій) природно вважати, що імовірності теж повинні мати такі ж властивості, як і частоти. Імовірність є числовою функцією, визначеною на алгебрі F подій, тобто кожній події А з F відповідає число Р(А) і для неї

справедливі умови:

1) ;

2) ;

3) якщо (тобто події несумісні), то .