Статически неопределимые комбинированные системы

В строительной механике под комбинированными понимают системы состоящие из комбинации рамных элементов, работающих в основном на изгиб и шарнирно-стержневых элементов, работающих на растяжение или сжатие.

Рассчитывают комбинированные системы, как правило, методом сил (если речь идет о ручном счете).

Особенностью расчета является определение коэффициентов системы канонических уравнений метода сил:

I слагаемое относится к рамным элементам, II – к шарнирно-стержневым элементам.

Первое слагаемое обычно определяют путем перемножения эпюр (используя для этого правило Верещагина или формулу Симпсона).

Второе слагаемое, как для статически неопределимых ферм:

Основную систему метода сил выбираем, разрезая 3 элемента фермы:

Для определения коэффициентов рассмотрим единичные и грузовое состояния основной системы :

Определяем коэффициенты, решаем систему и находим X₁, X₂,X₃.

После чего:

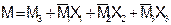
31.Расчёт неразрезных балок методом перемещений.

Степень линейной подвижности неразрезной балки всегда равна нулю.

Степень угловой подвижности равна числу промежуточных опор, т.е. для неразрезных балок число неизвестных метода перемещений определяется h=h_j; т.к. h_D=0.

И далее как в обычном методе перемещений

32. Расчёт неразрезных балок методом сил

Степень статической неопределимости неразрезной балки может быть определена по формуле Чебышева.

h=C_ОП+2Ш₀-2D, но учитывая, что Ш₀=0, а D=1, частный вид формулы:

h=C_ОП– 3

Исторически первоначально основную систему метода сил выбирали, отбрасывая «лишние» опорные связи:

Единичные эпюры при таком выборе основной системы распространяются на всю длину балки и ни один из единичных коэффициентов системы канонических уравнений не равен нулю.

В процессе практических расчетов убедились, что более рационально основную систему выбирать, вводя в промежуточные опорные сечения перерезывающие шарниры. В качестве неизвестных, при таком выборе основной системы, выступают опорные моменты. Единичные эпюры распространяются только на два соседних пролета и канонические уравнения метода сил значительно упрощаются, в каждом из них остается не более трех неизвестных.

33. Уравнение 3-х моментов. Общий вид ур-я . Порядок его применения.

Запишем каноническое уравнение метода сил для опоры n:

Тогда, подставляя значения найденных коэффициентов в систему канонических уравнений, получим

умножим полученное уравнение на 6

, (2)

и получаем уравнение трех моментов для расчета неразрезных балок. Это уравнение является частным видом канонических уравнений метода сил.

Для балок, имеющих постоянную жесткость по длине EI=const, что чаще всего встречается на практике, уравнение трех моментов запишется

(2¢)

Чтобы воспользоваться уравнением трех моментов, необходимо основную систему выбрать заменив заданную неразрезную балку системой однопролетных разрезных балок, в качестве неизвестных принять моменты над промежуточными опорами.

Опоры пронумеровать идя по балке слева направо. Пронумеровать пролеты, номер пролета должен соответствовать номеру правой опоры.

Для всех неизвестных опорных моментов записать уравнения трех моментов, построить грузовую эпюру, вычислить правые части уравнений и найти неизвестные опорные моменты.

Примечание:

Если одна из крайних опор – жесткое защемление, то со стороны этой опоры вводят фиктивный пролет, длина которого равна нулю.

35. Порядок расчёта неразрезных балок методом моментных фокусов

Если в неразрезной балке загружен только один пролет, то эпюра изгибающих моментов в остальных незагруженных пролетах представляет собой прямые линии, пересекающие ось балки. Опорные моменты, по мере удаления от загруженного пролета уменьшаются, эпюра как бы затухает.

Если рассматриваемые пролеты расположены левее загруженного, то нулевые точки смещены ближе к левым опорам и называются левыми фокусами F₁,F₂ и т.д., если пролеты расположены правее загруженного, то нулевые точки смещены ближе к правым опорам и называются правыми фокусами F₄,F₅ и т.д.

Каждый пролет имеет два фокуса (левый и правый), положение которых не зависит от действующей внешней нагрузки, а зависят только от геометрии балки.

Положения фокусных точек в пролете определяются их фокусными отношениями. Под фокусными отношениями понимаются отношения длин участков пролета, на которые делится этот пролет фокусной точкой. Например:

Или:

То есть: (3)

Используя уравнение трех моментов, выразим фокусные отношения через длины пролетов. Рассмотрим незагруженный участок балки с опорой n-1 по середине и запишем для нее уравнение трех моментов:

так как в пролетах l_n и l_n_-1нет нагрузки

w_n_-1=0; w_n=0.

разделим уравнение на M_n_-1

тогда

аналогично (4)

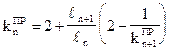
То есть фокусные отношения пролета n определяются через длины пролетов и фокусные отношения соседних пролетов.

– определяется через левое фокусное отношение предыдущего левого пролета, а – через правое фокусное отношение предыдущего правого пролета. Следовательно, фокусные отношения первых крайних пролетов должны быть известны.

36.Огибающие эпюры для неразрезных балок: основные положения, порядок построения

Нагрузки, действующие на сооружение, делятся на постоянные и временные.

Постоянные – это нагрузки, величина и место положения которых не меняется в процессе эксплуатации сооружения (например, собственный вес сооружения и т.п.).

Временные – это нагрузки, величина и место положения которых могут меняться в процессе эксплуатации сооружения (снеговые, полезные нагрузки и др.).

Для расчета неразрезных балок по условиям прочности, то есть для подбора их сечений, армирования и так далее, необходимо знать величины наибольших и наименьших изгибающих моментов не только на опорах и у середины пролета, но и в промежуточных сечениях. С этой целью для неразрезных балок строят огибающие эпюры. Кривая, соединяющая наибольшие положительные значения моментов называется огибающей M_max, а кривая, соединяющая наибольшие отрицательные значения моментов называется M_min.

Порядок построения огибающих эпюр:

1. Строится эпюра M для неразрезной балки от действия постоянных нагрузок (в РПР используя уравнения трех моментов).

2. Последовательно загружая каждый пролет и консоли балки временной нагрузкой, строят эпюры М от каждого отдельного загружения (используя метод моментных фокусов).

3. Для определения ординат огибающей эпюры M_max в каком либо сечении, необходимо к взятому со своим знаком значению момента от действия постоянной нагрузки, алгебраически прибавить все положительные значения моментов в данном сечении от отдельных загружений балки временной нагрузкой.

4. Ординаты огибающей M_min получают как алгебраическую сумму взятого со своим знаком значения момента от постоянной нагрузки и всех отрицательных значений момента в этом же сечении от загружений балки временной нагрузкой.

5. Значения M_max и M_min определяют в достаточном числе сечений, разбив предварительно рассматриваемый пролет балки на 5,10, или более частей (в зависимости от требуемой точности расчета).

6. Соединив полученные ординаты M_max и M_min, плавными кривыми, получаем огибающие M_max и M_min.

В случае необходимости, аналогично строим огибающие Q_max и Q_min.

37. Статически неопределимые арки , классификация примеры, методы расчёта

В строительстве применяют в основном два вида статически неопределимых арок:: двухшарнирные и бесшарнирные

Обе на рисунках арки являются распорными системами.

Расчет арок ведут методом сил, поскольку арка представляет собой кривой брус, часто переменного сечения по длине.

38.Двухшарнирные статически неопределимые арки: особенности расчёта, выбор основной с-мы, определение коэффициентов с-мы канонических ур-й.

Двухшарнирные арки выполняют как постоянного, так и переменного сечения по длине.

Двухшарнирные арки один раз статически неопределимы. Основную систему для их расчета выбирают, отбрасывая одну из горизонтальных опорных связей

Система канонических уравнений записывается:

Коэффициенты системы канонических уравнений определяют с помощью интеграла Мора (поскольку ось арки криволинейна, жесткость по длине пролета переменна), причем учитывается влияние на перемещения системы как изгибающих моментов, так и продольных сил:

Для пологих арок с высотой сечения , можно при определении коэффициентов системы канонических уравнений d₁₁ и D_1p пренебречь влиянием продольных сил:

В нашем случае, учитывая что

Если подинтегральные выражения сложные и не удается определить коэффициенты d₁₁ и D_1p непосредственным интегрированием, применяют численное интегрирование. Для этого арку разбивают на достаточное число участков и считая все компоненты подинтегральных выражений в пределах участков постоянными:

где n - число участков, на которое разбита арка.

39. Статически неопределимые двухшарнирные арки с затяжкой: особенности расчёта, выбор основной с-мы, определение коэффициентов с-мы канонических ур-й.

Арка с затяжкой один раз статически неопределима. Основную систему выбирают, разрезая затяжку.

Особенностью расчета таких арок является необходимость учитывать податливость затяжки при определении коэффициентов d₁₁ и D_1P.

Для пологих арок с высотой сечения :

учитывая, что площадь сечения затяжки постоянна по длине:

После определения

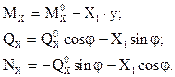
40. Бесшарнирные статически неопределимые арки : особенности расчёта, выбор основной с-мы, определение коэффициентов с-мы канонических ур-й.

Бесшарнирные арки могут выполнятся как постоянного, так и переменного сечения по длине.

Такая арка три раза статически неопределима. Арка симметрична, поэтому здесь основную систему рационально выбирать также симметричной, что позволит в дальнейшем упростить расчет

Канонические уравнения имеют вид:

Для пологих , гибких арок коэффициенты канонических уравнений можно определять учитывая влияние только изгибающих моментов, т.е. :

Учитывая, что X₁, X₂ - прямосимметричные, а X₃– обратносимметричное неизвестные:

И система из трех уравнений распадается на систему из двух уравнений и одно независимое уравнение:

Расчет можно еще более упростить, если в месте разреза арки ввести абсолютно жесткие консоли EI_K = ¥ :

Длину жестких консолей определяют из условия :

т.е. из условия:

Тогда, система канонических уравнений превратится в три независимых уравнения, каждое из которых содержит только одно неизвестное:

41. Смешанный метод расчета рам: основные принципы, общий вид системы канонических уравнений.

Встречаются системы, в которых можно выделить одну часть более удобную для расчета методом перемещений, а другая более удобна для расчета методом сил.

Метод, в котором принимают часть неизвестных метода сил, а часть – метода перемещений, называется смешанным.

42. Смешанный метод расчета рам: определение коэффициентов системы канонических уравнений.

Коэффициенты d_ik определяют как в методе сил, путем перемножения эпюр с помощью интеграла Мора:

;

для вычисления, которого можно использовать правило Верещагина или формулу Симпсона, d_ik = d_ki.

Коэффициенты r_ik- определяют как в обычном методе перемещений. Это реактивное усилие в связи i от единичного смещения связи k. r_ik = r_ki

Между коэффициентами со штрихами существует связь:

И проще определить который представляет собой реактивное усилие в связи i от действия силы X_k = 1 , а затем приравнять 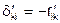. Либо определяют из эпюры перемещений.

43. Порядок расчета рам комбинированным методом

Порядок расчета симметричных рам комбинированным способом:

1. Произвольно действующую нагрузку преобразуют в прямо- и обратносимметричное загружение.

2. Независимо рассчитывают две рамы: а) на прямосимметричное загружение методом перемещений; б) на обратносимметричное загружение – методом сил.

3. Сумма двух полученных результирующих эпюр и даст нам эпюру M для заданного загружения:

44. Приближенные методы расчета: классификация, преимущества и недостатки.

Приближенные методы решения задач могут быть разбиты на две основные группы:

1. Вариационные методы, которые дают приближенные аналитические выражения искомой функции (функции перемещений или функции внутренних усилий).

2. Численные методы, которые дают значения искомой функции при тех или иных значениях аргумента.

Преимущество вариационных методов заключается в том, что задача сводится обычно к решению системы двух, трех, редко четырех уравнений, которые дают хорошее приближение к действительному состоянию сооружения. К их недостаткам следует отнести то, что возможности вариационных методов ограничены сложными контурами и сложными законами распределения внешней нагрузки, т.к. применение вариационных методов требует, чтобы было, хотя бы в приближенной форме, определено аналитическое выражение внешней нагрузки, деформированной упругой поверхности элемента и др. условий задачи.

Численные методы, в сравнении с вариационными, имеют более универсальный характер, т.к. не требуют аналитических выражений условий задачи. Однако численные методы обладают рядом недостатков. Так, для получения удовлетворительного решения они требуют нанесения на исследуемую область густой сетки или разбиения на достаточно большое число элементов, что неизбежно влечет за собой решение систем алгебраических уравнений с большим числом неизвестных, что становится возможным только при наличии ЭВМ. Кроме того, численные методы часто приводят к неточности решений, особенно в местах приложения сосредоточенных сил, при наличии острых углов, подкреплений и т.д., т.е. там, где нарушается гладкость полей переменных.

Весьма существенным недостатком численных методов является то, что они не дают аналитического выражения искомой функции, а, следовательно, для определения параметров напряженно-деформированного состояния в данной области приходится вычислять эти величины во всех узлах стыковки элементов, т.е. получать массу ненужной информации для тех областей, которые нас совершенно не интересуют.

45. Метод конечных элементов: основные предпосылки метода

Исторически возникновение МКЭ связано с идеей применения хорошо разработанных процедур для расчета статически неопределимых стержневых систем к решению континуальных задач.

Метод конечных элементов основан на мысленном представлении сплошного тела в виде совокупности отдельных конечных элементов, взаимодействующих между собой в конечном числе точек, которые в МКЭ принято называть узлами.

46. Метод конечных элементов: выбор основной системы.

Основную систему МКЭ получают, разбивая заданную систему на отдельные прямолинейные элементы, имеющие постоянную жесткость по длине. При наличии в системе криволинейных стержней или стержней с переменной жесткостью, их, с достаточной степенью точности, разбивают на участки, в пределах которых стержни считают прямолинейными, с усредненной постоянной жесткостью.

47. Матрица жесткости КЭ в местной системе осей координат: общий вид и основные принципы построения.

Для элемента с шестью степенями свободы (тип а) матрица жесткости будет иметь вид

[r]_j^’=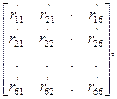

Принципы построения:

Формирование матрицы жесткости для элемента с шестью степенями свободы

Зададим последовательно единичные перемещения связям V₁, V₂...V_n.

В соответствие с законом Гука

Dl = Dl = V₁ = 1, N =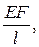

Расставляя реакции в соответствующие ячейки, получим матрицу жесткости для элемента с n степенями свободы.

Запишем матрицы жесткости для двух других типов элементов, формируя их аналогично предыдущей.

48. Матрица преобразований (направляющих косинусов): общие понятия.

Рассмотрим теперь КЭ в составе рамы, расположенный под углом a к оси Х в общей системе осей координат.

Необходимо перейти от матрицы реакций [r]^’_j в местной системе осей координат к матрице [r] в общей системе координат.

Задачу решаем следующим образом. В начале построим матрицу [c]_j, которая преобразует перемещения КЭ {z}_j в общей системе осей координат в перемещения {v}_j, по выражению

{v}_j = [c]_j {z}_j

V₁ = Z₁ cosa + Z₂ sina

V₂ = -Z₁ sina + Z₂ cosa

V₃ = Z₃

V₆ = Z₆

V₄ = Z₄ cosa + Z₅ sina

V₅ = -Z₄ sina + Z₅ cosa

В матричной форме приведенная выше запись будет иметь вид

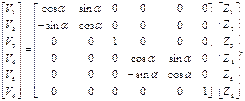
Так как мы рассматриваем плоские упругие системы, то векторы узловых усилий и узловых перемещений, как для отдельного элемента, так и для сооружения в целом, связаны между собой линейно

{S}_j^’ = [r]_j^’{V}_j - в местной системе осей координат.

{S}_j= [r]_j{Z}_j - в общей системе осей координат

[r]_j = [c]_j^T [r]_j^’ [c]_j - это выражение и является формулой для вычисления матрицы жесткости КЭ в общей системе осей координат.

При формировании матриц жесткости отдельных элементов [r]_j^’ должны быть зафиксированы начало и конец каждого стержня, так как от этого зависит знак угла a, определяющего ориентацию стержня в общей системе осей координат ХОY.

49. Порядок расчета стержневых систем методом конечных элементов.

1. Подготовительный этап включает в себя. Изображение расчетной схемы рассматриваемого сооружения, разбиение расчетной схемы на отдельные элементы, нумерацию узлов и элементов, выбор общей системы осей координат. Затем составляются исходные матрицы: матрицы жесткости отдельных элементов в местной системе осей координат [r]_j^’ и матрицы направляющих косинусов [c]_j , формируют вектор внешних нагрузок {P}, предварительно преобразовав вне узловую нагрузку к узловой.

2. Вычислительная часть расчета включает в себя. Вначале вычисляют матрицы жесткости

отдельных элементов в общей системе осей координат

-затем, из блоков этих матриц формируют матрицу жесткости [r] для сооружения в целом.

-вычисляют вектор перемещений узловых точек сооружения в общей системе осей координат.

Вектор узловых усилий для отдельных КЭ в общей системе осей координат

{S}_j = [r]_j {Z}_j

и в местной системе осей координат

{S}_j^’ = [c]_j {S}_j .

Результирующие усилия в узлах отдельных КЭ в местной системе осей координат, с учетом преобразований вне узловой нагрузки

3. Обработка результатов. Полученные усилия {S}_j^’прикладывают к узлам отдельных элементов и по ним строят результирующие эпюры M, Q, N.

⇐ Предыдущая 1 2 34