Главная | Обратная связь

Математична модель об’єкта

 

Математичну модель об’єкта будемо складати при таких допущеннях:

· густина рідини постійна і не залежить від температури;

· поперечні січення вздовж довжини резервуара постійні і мають форму круга;

· тиск , під яким рідина поступає в резервуар постійний;

· газ над рідиною в ємностях є ідеальним.

В основу математичної моделі покладемо рівняння матеріального балансу.

Для першої ємності:

. (7.1)

Для другої ємності:

, (7.2)

де М₁ і М₂ – маси рідини у першій та другій ємностях відповідно;

- масові витрати рідини.

Масова витрата рідини обчислюється за формулою:

,

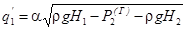де - тиск над рідиною в першій ємності.

Обчислимо тепер значення витрати, яка витікає з другої ємності.

.

де a₃ – гідравлічний опір витіканню рідини з ємності. Приймаємо a₃ =const.

Знаходимо значення витрати на вході другої ємності.

.

де a₂(U) - гідравлічний опір витіканню рідини з ємності, що залежить від

керуючої дії U.

Маса рідини в ємностях – це добуток густини рідини r на її об’єм V.

, i=1,2,

 

де , i=1,2.

Підставляючи значення в формули (7.1) і (7.2), отримуємо

, (7.3) (7.4)

 

Для ідеального газу маємо , де R – газова постійна; - маса газу над рідиною в другій ємності; m - молярна маса газу; Т – температура газу.

Оскільки T=const, і =const, то . З іншої сторони . Так як , то .

Отже,

. (7.5)

Підставляючи значення (7.5) в формули (7.3) і (7.4) приходимо до висновку, що

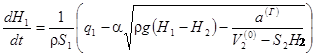(7.6)

 

,

 

(7.7)

Рівняння (7.6) і (7.7) утворюють математичну модель технологічного об’єкта.

Будемо вважати, що відхилення вихідних величин і від своїх усталених значень і незначні. Це означає, що нелінійні функції, які входять до рівнянь (7.6) і (7.7), можна розкласти в ряд Тейлора, обмежившись лише лінійними членами розкладу.

Припустимо, що , , 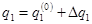і .

Введемо такі позначення:

,

 

.

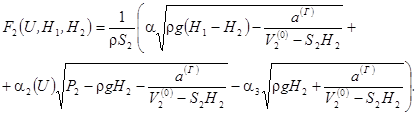Тоді

,

,

де

, ,

, ,

 

, .

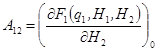Нехай:

.

Тоді отримаємо:

 

, (7.8)

. (7.9)

Отже, рівняння (7.8) і (7.9) утворюють лінеаризована математичну модель технологічного об’єкта.

Обчислимо параметри нелінійної математичної моделі, яка подана у вигляді диференціальних рівнянь (6.25) і (6.26).

Розглянемо статичний режим роботи об’єкта, коли і . Тоді

.

Звідси знаходимо

.

Враховуючи, що 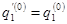, маємо

.

Тепер знаходимо

.

Оскільки , то

.

Аналогічно знаходимо

.

Знайдемо величину . Рівняння (6.24) запишемо для усталеного режиму

,

де - об’єм рідини в другій ємності, коли має місце стаціонарний режим роботи об’єкта.

Із останнього рівняння знаходимо

.

Параметри нелінійної моделі (7.6) і (7.7) обчислені з використанням програмного продукту MathCAD (рис. 7.2)

Статична характеристика регулюючого органу наведена на рис. 7.3. Для опису статичної характеристики регулюючого органу використаємо поліном Лагранжа [2]. Вихідні дані для апроксимації отримуємо із графіка залежності . Такі дані носять назву детермінованих породжені власними функціями виконавчих органів, аналітичний вид яких нам невідомий. Функцією апроксимації називають деяку залежність, яка у відповідності з певним критерієм замінює власну функцію. Критерій наближення формулюється як вимога, щоб у заданих вузлових точках, значення власної функції і функції апроксимації співпадали.

В такому задача апроксимації формулюється наступним чином. Нехай N – число вузлів апроксимації, а n=N-1 – степінь інтерполяційного полінома. Необхідно знайти поліном степені п, щоб в точках апроксимації його значення співпадали зі значеннями власної функції.

Розв'язок поставленої задачі приводить до такого інтерполяційного полінома Лагранжа

 

 

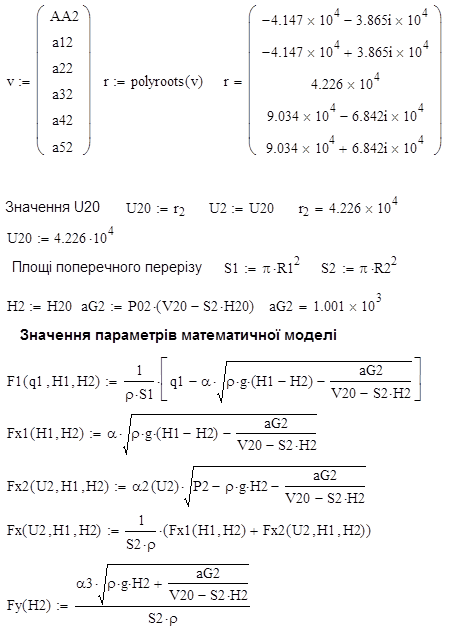
Рисунок 7. 2 – Програма розрахунку параметрів гідравлічного об’єкта

 

 

.

В нашому випадку для побудови інтерполяційного

 

 

Рисунок 7.3 – Статична характеристика регулюючого органу

 

полінома використано N=6 вузлів. Необхідні дані для побудови інтерполяційного полінома занесені в табл. 7.1.

 

Таблиця 7.1 – Вихідні дані для побудови інтерполяційного полінома

 

		0,02	0,04	0,06	0,08	0,1
	0,1	0,092	0,079	0,062	0,039

Для інтерполяції ми вибрали N=6 вузлів, що приводить до такого інтерполяційного полінома:

. (7.10)

Оскільки для статичного режиму має місце співвідношення

,

то для обчислення 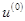необхідно розв’язати рівняння

, (7.11)

де .

Коефіцієнти інтерполяційного полінома (7.10) обчислені, у відповідності з програмою Inter.bas, текст якої наведений в [2, част. 3, с. 156 - 157]. Рівняння (7.11) розв’язано з використанням програмного продукту MathCAD (див. рис. 7.2).

Обчислення параметрів лінеаризованої моделі математичної моделі (7.8) і (7.9) здійснено за допомогою програмного продукту MathCAD. Результати такого розрахунку відображені на рис. 7.2.