 |
|
Моменти інерції круга
При визначенні осьових моментів інерції круга зручніше спочатку знайти полярний момент інерції відносно його центра. Для цього візьмемо круг радіусом r (рис. 52) та розіб'ємо його на нескінченно вузькі концентричні кільця шириною dρ. Взявши одне із кілець радіусом ρ, визначимо його полярний момент інерції:
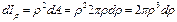
де 
Для знаходження полярного момента інерції круга необхідно взяти інтеграл цього значення. 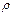 в цьому випадку змінюється від 0 до r.
в цьому випадку змінюється від 0 до r.
 (72)
(72)
Виражаючи полярний момент інерції через діаметр, отримаємо:

або остаточно:
 (72')
(72')
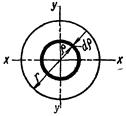
Рис. 52
Так як круг симетричний відносно будь-якого діаметру осьові моменти інерції відносно будь-яких осей, що проходять через центр круга, однакові, тобто  , а так як
, а так як  , то величина осьового моменту інерції площі круга відносно будь-якої осі, що проходить через центр круга, дорівнює половині полярного момента інерції, тобто
, то величина осьового моменту інерції площі круга відносно будь-якої осі, що проходить через центр круга, дорівнює половині полярного момента інерції, тобто
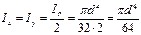
або остаточно
 (73)
(73)
Осьовий момент кругового кільця.
Осьовий момент кругового кільця визначається як різниця осьових моментів інерції великого круга діаметром D та малого круга діаметром d (Рис.53)

Рис. 53

остаточно
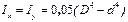 (73')
(73')
Осьовий момент інерції трикутника
Розбиваємо площу трикутника на нескінченно вузькі смужки шириною dу та виділимо одну з них, що знаходиться на відстані у від осі х1 (рис. 54). Із подібності трикутників АВС та аВс визначаємо х:
 ;
; 
площа елементарної смужки:

Тоді осьовий момент інерції площі трикутника відносно осі х1:
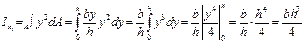
остаточно:
 (74)
(74)
Таким же чином знаходять моменти

Рис. 54
інерції трикутника відносно осі х2, що співпадає з його основою, і відносно центральної осі х.
 74')
74')
 (74")
(74")
§32. ГОЛОВНІ ОСІ ІНЕРЦІЇ ТА ГОЛОВНІ МОМЕНТИ ІНЕРЦІЇ. ЗАЛЕЖНІСТЬ МІЖ ОСЬОВИМИ МОМЕНТАМИ ІНЕРЦІЇВІДНОСНО ПАРАЛЕЛЬНИХ ОСЕЙ
В цьому курсі ми будемо розглядати тільки ті перерізи, що мають вісь симетрії. Якщо в перерізі вісь симетрії прийнята за вісь х або у, то відцентровий момент інерції відносно цієї осі дорівнює нулю, так як в цьому випадку кожному елементу dА з додатним у відповідає рівний і симетрично розміщений елемент dА' з від'ємним у. Елементарні добутки х·у·dА взаємно знищуються і інтеграл  перетворюється в нуль.
перетворюється в нуль.
Покажемо, що для будь-якої точки довільного плоского перерізу можна знайти такі дві взаємно перпендикулярні осі, відносно яких відцентровий момент інерції буде дорівнювати нулю. Нехай для довільного перерізу координатні осі повернені на 90°, тоді вони займуть положення х' та у' (рис. 55).
Якщо тепер виразити нові координати через старі, отримаємо
 ;
; 
Тоді відцентровий момент інерції відносно нового положення осей

Тобто ми бачимо, що при повертанні осей на 90° відцентровий момент інерції змінює знак. Тому завжди буде і таке положення осей, відносно яких величина відцентрового моменту інерції дорівнює нулю.

Рис. 55
Осі, відносно яких відцентровий момент інерції плоского перерізу дорівнює нулю, називаються головними осями інерції.
Якщо початок координат головних осей співпадає з центром ваги перерізу, то такі осі називаються головними центральними осями інерції, а моменти інерції відносно таких осей називаються головними центральними моментами інерції.
В подальшому, для простоти, будемо називати їх головними осями та головними моментами.
Головні моменти інерції мають граничні (екстремальні) значення: один з них Imax, а другий Іmin.
Осі симетрії будь-якого перерізу є головними осями інерції. У таких перерізів як тавр, швелер тощо, вісь симетрії є головною віссю інерції. Другою головною віссю є перпендикулярна до неї вісь, що проходить через центр ваги перерізу.
Щоб визначити момент інерції якогось перерізу відносно будь-якої осі, необхідно знати залежність між моментами інерції цього перерізу відносно двох паралельних осей, із яких одна є центральною віссю.
Нехай у якомусь довільному перерізі площею А (рис. 56) вісь х буде центральною, а вісь х1 – паралельною їй на відстані а. Виділимо в перерізі елементарну площадку dА на відстані у від осі х. Тоді момент інерції відносно цієї осі дорівнює:

Знайдемо момент інерції відносно осі х1.
Відстань y1 елементарної площадки до осі х1 буде дорівнювати у + а, тобто

Тоді

В отриманому виразі перший інтеграл є осьовим моментом інерції відносно осі х, що проходить через центр ваги перерізу, тобто 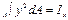 : другий інтеграл є статичним моментом всієї площі перерізу відносно осі х, тобто
: другий інтеграл є статичним моментом всієї площі перерізу відносно осі х, тобто 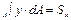 . А так як статичний момент площі плоскої фігури відносно центральної осі дорівнює нулю, то другий доданок дорівнює нулю. Останній інтеграл
. А так як статичний момент площі плоскої фігури відносно центральної осі дорівнює нулю, то другий доданок дорівнює нулю. Останній інтеграл  виражає собою площу всього перерізу А.
виражає собою площу всього перерізу А.
Таким чином, момент інерції перерізу відносно осі х1 дорівнює
 (75)
(75)

Рис. 56
Ця формула читається так: момент інерції площі перерізу відносно любої осі дорівнює моменту інерції відносно осі, їй паралельний, що проходить через центр ваги перерізу, плюс добуток площі цього перерізу на квадрат відстані між осями.
За допомогою цієї формули можна знаходити моменти інерції будь-якого складного перерізу, так як момент інерції всього перерізу, відносно якоїсь осі, дорівнює сумі моментів інерції частин перерізу відносно цієї ж осі.
Приклад 19. Визначити момент інерції поперечного перерізу (рис. 57) збірної плити перекриття відносно центральної осі х.

Рис. 57(рис. 2.97, Збірник Утіліт, с. 153)
Розв'язок. Плита перекриття має форму прямокутника. Момент інерції цього перерізу відносно осі х (вона є головного віссю) знаходимо за формулою (71).

Але переріз ослаблений п'ятьма отворами, моменти інерції яких ми повинні виключити. Моменти інерції круглого отвору знаходимо за формулою (73), тобто
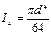
Тоді момент інерції всього перерізу дорівнює:

Приклад 20.Визначити головні центральні моменти інерції перерізу (рис. 58).

Рис. 58
Розв'язок. Знайдемо положення головних осей інерції перерізу. Переріз має вісь симетрії, вона співпадає з власною віссю двотавра у1. Позначимо головну вісь великою буквою У. Друга головна вісь буде перпендикулярна осі У та проходити через центр ваги перерізу. Знайдемо положення центру ваги перерізу. Для цього проведемо та позначимо власні осі кожного елемента перерізу. За допоміжні осі, для знаходження центра ваги, приймемо власні осі двотавра х1 та у1, так як власна вісь двотавра у1 є віссю симетрії перерізу Y. Координати центра ваги знаходимо за формулами:

Координата хс= 0, так як центр ваги лежить на осі симетрії, тобто на осі у1. Необхідні дані для знаходження координати yс зведемо в таблицю.
| № | Ескіз | 
| 
| 
| |
| ² | 26,8 | ||||
| Π | 20,7 | -11,94 |
 = – 5,2 см
= – 5,2 см
Покажемо центр ваги на схемі та проведемо другу головну вісь Х. Використовуючи зв'язок між моментами інерції відносно паралельних осей, знайдемо головний момент інерції відносно осі Х.

де  – момент інерції двотавра відносно власної осі х1,
– момент інерції двотавра відносно власної осі х1,
 – момент інерції швелера відносно власної осі у2.
– момент інерції швелера відносно власної осі у2.

Головний момент інерції відносно осі У знаходимо як суму моментів інерції двотавра і швелера, так як їх власні осі співпадають з головною віссю У.
 ,
,
де 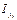 – момент інерції двотавра відносно власної осі y1,
– момент інерції двотавра відносно власної осі y1,
 – момент інерції швелера відносно власної осі х2.
– момент інерції швелера відносно власної осі х2.
Остаточно: 

Питання для самоконтролю
1. Як практично знаходиться статичний момент площі плоскої фігури відносно осі?
2. Чому дорівнює статичний момент плоскої фігури відносно осі, що проходить через центр ваги?
3. Що називається осьовим, полярним, відцентрованим моментами інерції? Яка їх одиниця вимірювання?
4. Які моменти інерції завжди додатні?
5. Чому дорівнює осьовий момент прямокутника відносно його осей симетрії?
6. Чому дорівнюють осьові моменти інерції круга та кільця?
7. Які осі перерізу називаються головними?
8. Які моменти інерції називаються головними?