 |
|
РОЗДІЛ 4. ПЛОСКа ЗАДАЧА ТЕОРІЇ ПРУЖНОСТІ
У ПОЛЯРНИХ КООРДИНАТАХ
Основні рівняння
При рішенні плоскої задачі зустрічаються тіла, обмежені поверхнями кругового циліндра і радіально розбіжними площинами. У цих випадках перехід від декартовой системи координат до полярної значно спpощує рішення.
У полярній системі координат положення будь-якої точки на площині визначається двома величинами: радіус-вектором 
і полярним кутом 
, відлічуваним від початкового радіуса-вектора 
. Розглянемо основні рівняння плоскої задачі в полярних координатах: диференціальні рівняння рівноваги, рівняння нерозривності деформацій, формули Коші і формули узагальненого закону Гука.
Виріжемо із пластинки товщиною, рівною одиниці, елемент 
(рис. 4.1). Для цього проведемо радіус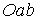 
під довільним кутом 
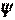до початкового радіус-вектору, потім дамо куту нескінченно мале збільшення 
й проведемо радіус 
. Довільним радіусом 
проведемо дугу 
, потім дамо радіусу збільшення 
й проведемо другу дугу — 
. Сторони отриманого елемента мають наступні розміри:
, 
, 
.
Рис. 4.1. Елемент пластинки в полярних координатах
На границях елемента діють наступні складові напружень: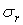 
— радіальне нормальне напруження; 
— тангенціальне нормальне напруження;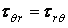 
— дотичні напруження; 
і 
— складові об'ємної сили.
Складемо рівняння проекцій всіх сил на осі й :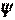
При спрощенні врахуємо, що через малість кута можна прийняти
.
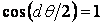Тоді, відкидаючи величини третього порядку малості і ділячи обидва рівняння на площу елемента 
, одержуємо диференціальні рівняння рівноваги для плоскої задачі в полярній системі координат:
| (4.1) |
Особливістю цих рівнянь у порівнянні з умовами рівноваги для плоскої задачі в декартових координатах є наявність у знаменнику величини . Чим ближче до початку координат (полюсу) розташована розглянута точка, тим швидше будуть зростати доданки, що містять множник 
, тому що необмежено убуває. Тому рівняння (4.1) неприйнятні для точок, що лежать поблизу полюса.
Перетворимо до полярних координат рівняння нерозривності деформацій. У декартових координатах воно записувалося у вигляді
 .
| (а) |
Сума нормальних напружень по двох взаємно перпендикулярних площадках у плоскої задачі є інваріантом. Дійсно, підставляючи в перший інваріант напруженого стану 
, одержимо, що при узагальненому плоскому напруженому стані інваріантною величиною є
При плоскій деформації напруження
і інваріантною величиною є
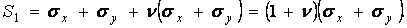
Таким чином, у плоскої задачі в кожній точці сума нормальних напружень по двох взаємно перпендикулярних площадках є величина постійна, і можна скласти наступну тотожність:
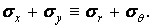
Заміняючи з його допомогою напруження у формулі (а), одержуємо рівняння нерозривності деформацій для плоскої задачі в полярній системі координат:
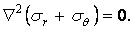
| (б) |
Однак оператор Лапласа в полярній системі має інший вид, чим у декартовій. Замінимо декартови координати на полярні. Для цього на рис. 4.1 вісь 
сполучимо з початковим радіус-вектором , а вісь 
направимо донизу. У цьому випадку полярні координати пов'язані з декартовими наступними залежностями:
 
| (4.2) |
Диференціюючи ці залежності по й і з огляду на, що 
, 
, знаходимо
| (в) |
Обчислюємо перші похідні по й довільній функції 
Використовуючи вираз (в), одержуємо
| (г) |
Аналогічно обчислюємо другі похідні тої ж функції:
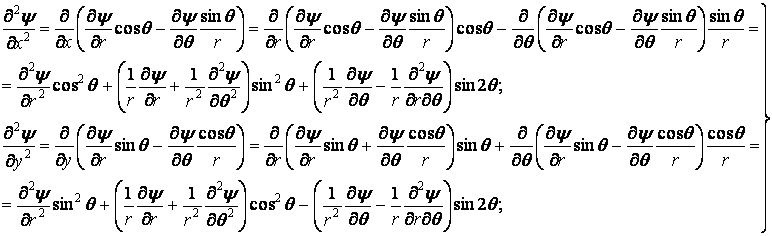
| (д) |
Сполучимо вісь із радіус-вектором . У цьому випадку 
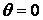й похідні в декартової системі координат (г) і (д) виразяться через похідні в полярній системі в такий спосіб:
| (е) |
Тоді оператор Лапласа приймає вид
| (ж) |
Використовуючи це вираження в рівнянні (б), одержимо розгорнуте рівняння нерозривності деформацій для плоскої задачі в полярній системі координат:
| (4.3) |
Виразимо тепер у цій системі геометричні співвідношення Коші. Позначимо складову переміщення уздовж осі через 
, а уздовж осі — через 
.
На рис. 4.2 зображений елемент до деформування й положення точок 
, 
і 
після деформування.
Рис. 4.2. Елемент пластинки до і після деформування
Відносне подовження в напрямку за рахунок переміщення знаходимо аналогічно тому, як це зроблено в декартовій системі координат:
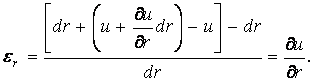
| (з) |
Відносне подовження уздовж осі 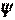залежить як від складової переміщення , так і від складової . У першому випадку
у другому, за аналогією з формулою (з),
Тут елемент дуги 
замінений на добуток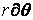 
. Сумарне подовження
| (и) |
Кутова деформація в розглянутій площині
де   
| (к) |
Таким чином, геометричні співвідношення Коші в полярній системі координат утворять систему рівнянь (з), (і), (к):
| (4.4) |
Формули закону Гука для узагальненого плоского напруженого стану в полярних координатах зберігають такий же вид, як і в декартовій системі [див. (3.8)], при заміні індексів і на й :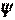
| (4.5) |
У випадку плоскої деформації пружні постійні 
й 
у формулах (4.5) повинні бути замінені відповідно на пружні постійні 
й 
відповідно до формул (3.9).