 |
|
Направляющий вектор прямой
Определение 11.1. Направляющим вектором прямой будем называть любой вектор, отличный от нулевого, который параллелен данной прямой или лежит на ней. 
Обозначается: 
.
Пусть точка 
- начальная точка, т.е. с известными координатами, точка 
- произвольная точка пространства. Рассмотрим вектор 
и найдём
его координаты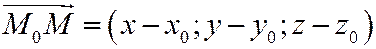 
. Точка М будет принадлежать прямой l тогда и только тогда, когда вектор коллинеарен вектору 
(т.е. их координаты пропорциональны).
- получили каноническое уравнение прямой, где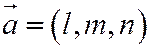 
- направляющий вектор прямой, 
- известная точка, лежащая на прямой.
Приведение общего уравнения прямой в пространстве к каноническому виду
Пусть прямая l задана: 
(11.2)
Тогда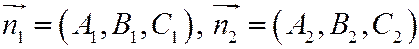 
- нормальные векторы плоскостей 
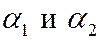соответственно.
Чтобы привести общее уравнение прямой к каноническому виду, нужно:
1) знать какую-нибудь точку 
;
2) знать направляющий вектор прямой l, т.к. 
.
Пример 11.1. Привести к каноническому виду уравнение прямой: 
1) Положим 
, тогда 
, 
По формуле Крамера находим: 
. Следовательно, точка 
- начальная точка.
2) 
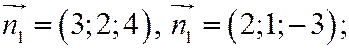
Следовательно, искомое уравнение: 
.
Параметрическое уравнение прямой
Пусть l задана каноническим уравнением: 
. Обозначим равенство трех отношений через t. Преобразовав уравнение, получим:
- параметрическое уравнение прямой(11.3)
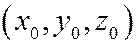- координаты начальной точки 
;
- координаты направляющего вектора, t – параметр.
Параметрическое уравнение прямой удобно применять в задачах на нахождение точки пересечения прямой и плоскости.
Пример 11.2. Найти точку пересечения прямой l и плоскости a. 
, 
.
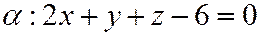Запишем уравнение прямой в параметрическом виде: 
Подставим эти значения 
в уравнение плоскости: 
,
- параметр определили и подставим его в систему: 
Искомая точка 
.
Уравнение прямой, проходящей через две точки в пространстве
-две точки пространства. По аналогии с прямой на плоскости:
(11.4)