 |
|
Гиперболический параболоид
Определение.Поверхность, которая в декартовой системе координат определяется уравнением:  (12.7)
(12.7)
Называется гиперболическим параболоидом.
Исследуем уравнение (12.7).
Рассмотрим сечение плоскостью 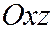 , т.е.
, т.е. 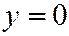 .
.
 - парабола симметрична относительно оси
- парабола симметрична относительно оси  с вершнами в начале координат. Теперь рассмотрим сечения (12.7) плоскости, параллельной
с вершнами в начале координат. Теперь рассмотрим сечения (12.7) плоскости, параллельной 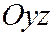 .
.
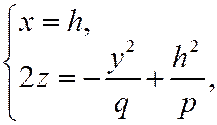 - парабола, ветви которой направлены вниз и симметрично относительно
- парабола, ветви которой направлены вниз и симметрично относительно  . Все эти параболы будут находится, вершинами на восходящей параболе
. Все эти параболы будут находится, вершинами на восходящей параболе 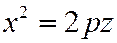 , и как бы перемещаться вершиной по линии предыдущей параболы. Сечение гиперболического параболоида плоскостями, параллельными
, и как бы перемещаться вершиной по линии предыдущей параболы. Сечение гиперболического параболоида плоскостями, параллельными  .
.
 - гипербола, симметричная относительно плоскостей
- гипербола, симметричная относительно плоскостей  .
.
Вывод: Гиперболический параболоид имеет форму седла, обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат называется вершинойгиперболического параболоида. Числа  называются его параметрами.
называются его параметрами.
Конус
Определение. Поверхность, которая определяется уравнением:
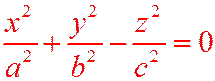 (12.8)
(12.8)
состоит из прямых, проходящих через одну точку, именно, через начало координат и называется конусом.
Заметим, что (12.8) однородно, все его члены имеют одну и ту же степень 2. Точка 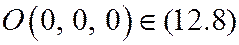 .
.
 Теорема:Если некоторая точка
Теорема:Если некоторая точка 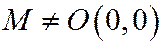 лежит на поверхности (12.8), то все точки прямой, которые проходят через начало координат и точку М, также лежат на этой поверхности.
лежит на поверхности (12.8), то все точки прямой, которые проходят через начало координат и точку М, также лежат на этой поверхности.
Прямые, из которых составлен конус, называются его образующими  - вершина. Проведем сечение
- вершина. Проведем сечение 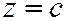 .
.
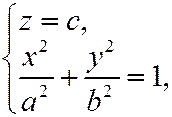 - эллипс с полуосями
- эллипс с полуосями  .
.
Если  , то в сечении окружность и называется круглым конусом. Рассмотрим уравнение:
, то в сечении окружность и называется круглым конусом. Рассмотрим уравнение:  (12.9)
(12.9)
Это уравнение определяет единственную действительную точку  . Однако, ввиду аналогии с уравнением (12.8) его часто называют мнимого конуса.
. Однако, ввиду аналогии с уравнением (12.8) его часто называют мнимого конуса.
| №/п | Рисунок | Название поверхности | Уравнение поверхности |

| Эллипсоид | 
| |
| Мнимый эллипсоид | 
|

| Однополостный гиперболоид | 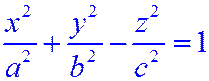
| |
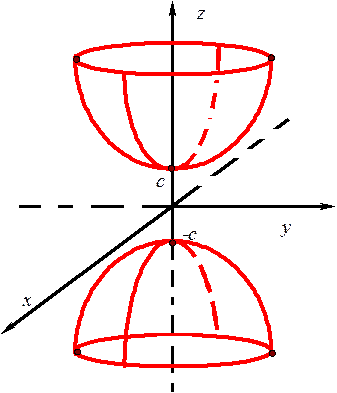
| Двухполостный гиперболоид | 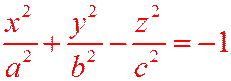
|

| Эллиптический параболоид | 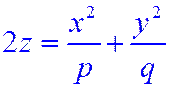
| |

| Гиперболический параболоид | 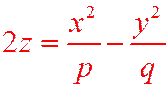
|

| Конус | 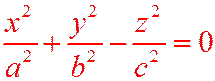
| |
| Мнимый конус | 
|
Обобщённая таблица по теме: «Плоскость. Прямая в пространстве»
| №/п | Условия | Уравнение |
| Векторное уравнение плоскости | 
| |
| Векторное уравнение плоскости в координатной форме |
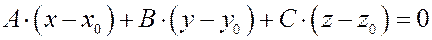
| |
| Общее уравнение плоскости | 
| |
Угол между двумя плоскостями, заданными нормальными векторами 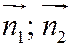 прямых прямых 
| 
| |
Угол между двумя плоскостями, заданными общими уравнениями 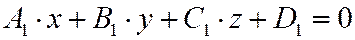 и и 
| 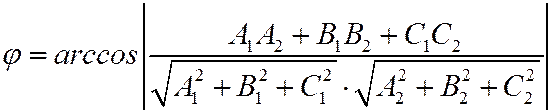
| |
Условие параллельности двух плоскостей, заданными общими уравнениями 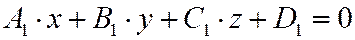 
|

| |
Условие перпендикулярности двух плоскостей, заданными общими уравнениями 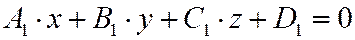 
| 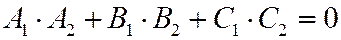
| |
| Векторно – параметрическое уравнение прямой в пространстве | 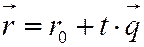
| |
Параметрическое уравнение
прямой в пространстве
 ; ; 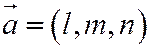 - координаты направляющего вектора, t – параметр. - координаты направляющего вектора, t – параметр.
| 
| |
| Уравнение плоскости в отрезках | 
| |
Уравнение плоскости, проходящее через три заданные точки

| 
| |
Расстояние от точки  до плоскости до плоскости  . .
|
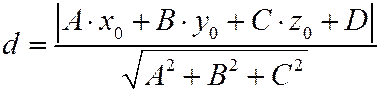
| |
Каноническое уравнение прямойв пространстве,проходящей через точку  параллельно вектору параллельно вектору 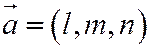
|

| |
Направляющие косинусы прямой в пространстве, где направляющий вектор прямой 
| 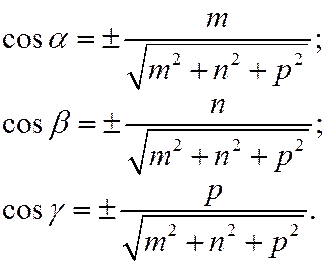
| |
Условие параллельности двух прямых в пространстве,
заданными каноническими уравнениями
 и и 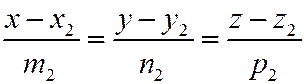
|

| |
Условие перпендикулярности двух прямых в пространстве,
заданными каноническими уравнениями
 и и
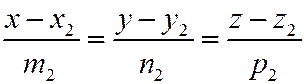
| 
| |
Угол между двумя прямыми в пространстве 
|
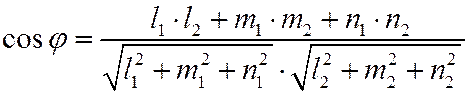
| |
Угол между прямой и плоскостью определяется
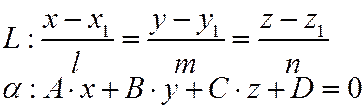
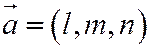 - направляющий вектор, - направляющий вектор, 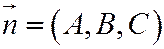 - нормаль к плоскости. - нормаль к плоскости.
|
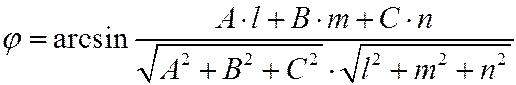
| |
Условие параллельности прямой  и плоскости в пространстве и плоскости в пространстве

| 
| |
Условие перпендикулярности прямой  и плоскости в пространстве и плоскости в пространстве 
| 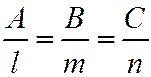
| |
Условия, при которых прямая  принадлежит плоскости принадлежит плоскости 
| 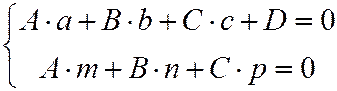
| |
Уравнение пучка плоскостей, проходящих через данную прямую 
|

|