 |
|
Угол между двумя прямыми в пространстве
Пусть заданы прямые 
Тогда угол определяется по формуле: 
.
Условия параллельности и перпендикулярности двух прямых в пространстве
Пусть две прямые заданы каноническим видом. Их направляющие векторы: 
.
Теорема 11.1: Две прямые параллельны тогда и только тогда, когда 
т.е. 
.
Теорема 11.2: Две прямые перпендикулярны тогда и только тогда, когда 
, т.е. 
, т.е. 
.
Угол между прямой и плоскостью. Параллельность прямой и плоскости, перпендикулярность прямой и плоскости
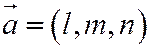- направляющий вектор, 
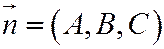- нормаль к плоскости.
Угол между прямой и плоскостью определяется по формуле:
Условие параллельности прямой и плоскости в пространстве:
.
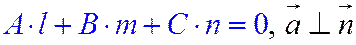Условие перпендикулярности прямой и плоскости в пространстве:
.
Поверхности второго порядка
Поверхности являются пространственными аналогами кривых второго порядка на плоскости.
Эллипсоид
Определение. Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением:
- каноническое уравнение эллипсоида. (12.1)
Рассмотрим форму эллипсоида с помощью «метода параллельных сечений». Рассмотрим сечения данного эллипсоида плоскостями, параллельными Оху, т.е. z=h. Линия, которая получается в сечении, определяется двумя уравнениями:
(12.2)
Если:
1) 
, то плоскость z=h пересекает эллипсоид (12.1) по эллипсу с полуосями: 
.
2) Величины 
имеют наибольшие значения при h=0, иначе говоря, самый крупный эллипсоид получается при сечении координатной плоскостью z=0.
3) При возрастании 
величины уменьшаются.
4) При 
величины обращаются в 0, т.е. сечение эллипса вырождается в точку 
.
5) При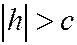 
, уравнения (12.2) определяют мнимый эллипс, т.е. плоскость z=h с данным эллипсоидом не встречается совсем.
Совершенно аналогично рассматриваются сечения эллипсоида плоскостями, параллельными 
.
Таким образом, вывод: эллипсоид есть замкнутая овальная поверхность, обладающая тремя взаимно перпендикулярными плоскостями симметрии. Величины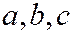 
называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехостным.
При 
эллипсоид, можно рассмотреть как поверхность, образованную вращением эллипса вокруг одной из его осей: если эллипсоид образован вращением вокруг его большой оси, он называется вытянутым эллипсоидом вращения, если вокруг меньшей оси – то сжатым эллипсоидом вращения.
В случае 
имеем сферу.
Уравнение 
, ввиду аналогии с (12.1) называется уравнением мнимого эллипсоида: (12.3)
Гиперболоид
Определение.Однополостным гиперболоидом называется поверхность, которая в данной декартовой системе координат определяется уравнением: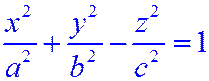 
(12.4)
Определение.Двухполостным гиперболоидом называется поверхность, определяемая уравнением: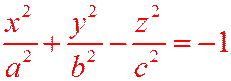 
(12.5)