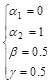 |
|
Bывод формулы метода Рунге-Кутты второго порядка
Методы Рунге-Кутты являются одношаговыми методами решения систем обыкновенных дифференциальных уравнений, представленными в нормальной форме Коши. При этом точное решение дифференциального уравнения описывается формулой:
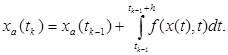(1.8)
В методах Рунге – Кутты интеграл заменяется линейной комбинацией значений подинтегральной функции, вычисленных при разных значениях аргумента
,
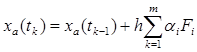где m – порядок метода.
благодаря чему все методы Рунге – Кутты можно представить в следующем общем виде:
Из вышеуказанных общих формул получают формулы метода Рунге-Кутты 2-ого порядка (m=2):
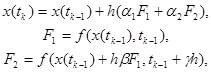(1.9)
Для определения метода необходимо определить значения коэффициентов: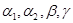 
. Для этого интеграл, заменяемый линейной комбинацией значений подынтегральной функции, вычисленных при разных значениях аргумента, представим в виде частичной суммы ряда Тейлора
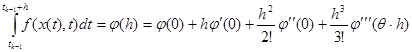. (1.10)
Остаточный член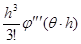 
есть ни что иное как локальная алгоритмическая ошибка
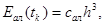(1.11)
где сал – коэффициент пропорциональности, слабо зависящий от h.
Окончательно получим выражения производных в нуле:
,
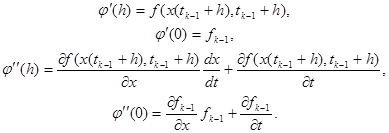
Дифференцирование можно продолжать, однако очевидно что коэффициенты будут выражаться через форму Коши (1.6) в tk-1, и ее производной по х(t), и по t. Подставляя, полученные выше результаты в (1.8), получаем разностную схему численного интегрирования ОДУ:
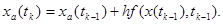(1.12)
Осталось определить значения коэффициентов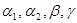 
формул (1.9). Для этого введем вспомогательную функцию: 
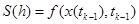, выражение (1.12) примет вид:
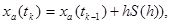
где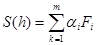 
.
Коэффициенты a, b, g должны удовлетворять условию:
, 
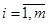, (1.13)
где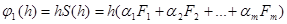 
.
Для нахождения коэффициентов необходимо определить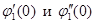 
. Продифференцируем по h, учитывая, что S(h) – сложная функция:
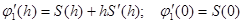
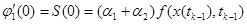
Из условия (1.13) получаем:
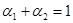(1.14)
Находим 2-ю производную
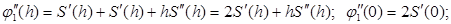
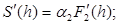
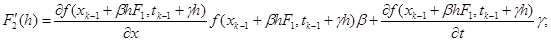
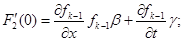
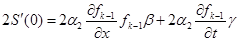
Из условия (1.13) получим второе и третье уравнения:
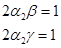(1.15)
Объединив (1.14) и (1.15) получим СЛАУ
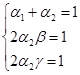
Полученная СЛАУ имеет бесконечное число решений. Нужное решение выбираем исходя из метода, указанного в варианте задания. В данной курсовой работе используется следующее решение:
