 |
|
Сравнительный анализ методов Рунге – Кутты при различных требованиях к точности вычислений
При интегрировании уравнения (1.1) основное время занимает вычисление правой части. Поэтому в качестве оценки затрат машинного времени естественно принять количество вычислений правых частей уравнений (1.6) на всём отрезке интегрирования. Эту величину легко определить, умножив количество шагов интегрирования N на порядок метода m .
На рисунке 3.7 представлен график зависимости оценки ошибки интегрирования от количества вычислений правой части.

Рисунок 3.7 – График зависимости оценки ошибки интегрирования от количества вычислений правой части
Из графика видно, что на интервале шага [1;0.001] , где влияние вычислительной ошибки не велико, при одинаковых вычислительных затратах, метод Рунге – Кутты 4-го порядка, позволяет получить ошибку, значительно меньшую, чем метод 2-го порядка.
Так же из графика можно увидеть, что существует такое значение шага, после которого дальнейшее его уменьшение ведёт только к увеличению вычислительных затрат и росту оценки ошибки, программа тратит машинное время впустую.
ЗАКЛЮЧЕНИЕ
В ходе работы была составлена и отлажена программа для интегрирования обыкновенных дифференциальных уравнений и с помощью этой программы проведено ряд экспериментальных исследований свойств методов Рунге-Кутты второго и четвёртого порядка.
На определённом интервале значений шага интегрирования, с уменьшением шага ошибка интегрирования уменьшается (что согласуется с теорией), но на остальном интервале с уменьшением шага интегрирования ошибка увеличивается. Это связано с ростом числа вычислений и, следовательно, увеличением ошибки вычислений.
На интервале значений шага интегрирования, где влияние ошибки вычисления не велико, метод 4-го порядка даёт ошибку гораздо меньшую, чем метод 2-го порядка.
Гипотеза Рунге подтверждается только для таких значений шага, при которых влияние вычислительной ошибки незначительно. При дальнейшем уменьшении шага, пропорциональность нарушается, это объясняется тем, что гипотеза Рунге не учитывает влияние вычислительной ошибки. Коэффициент пропорциональности для метода четвертого порядка на несколько порядков меньше, чем для метода второго порядка, что согласуется с теорией.
Для значения шага h = 2, наблюдается лавинообразный рост ошибки, что объясняется тем, что при заданном значении шага нарушается устойчивость алгоритма как для метода второго, так и для метода четвёртого порядка. На рис.3.4 наблюдается заметное отклонение решения, полученного численно, от точного значения искомой функции. Но даже для этого значения шага, наблюдается значительная разница между ошибками для методов второго и четвёртого порядков.
Для значения шага h = 1e-3, можно заметить более плавный рост ошибки, особенно для метода четвертого порядка, это объясняется тем, что влияние алгоритмической ошибки уменьшается, а вычислительной - возрастает. Графики точного значения функции и приближенных значений, полученных численно, совпадают, что говорит о хорошей точности методов Рунге – Кутты второго и четвертого порядков.
Для значения шага h = 1e- 7 графики ошибок для методов второго и четвертого порядков совпадают. Это можно объяснить тем, что для данного значения шага алгоритмическая ошибка мала для обоих методов и основное влияние на локальную ошибку оказывает вычислительная погрешность. Графики точного значения функции и приближенных значений, полученных численно, совпадают, что говорит о хорошей точности методов Рунге – Кутты второго и четвертого порядков. На интервале шага, где влияние вычислительной ошибки не велико, при одинаковых вычислительных затратах, метод Рунге – Кутты 4-го порядка, позволяет получить ошибку, значительно меньшую, чем метод 2-го порядка.
Существует такое значение шага, после которого дальнейшее его уменьшение ведёт только к увеличению вычислительных затрат и росту оценки ошибки, программа тратит машинное время впустую.
ПЕРЕЧЕНЬ ССЫЛОК
1. Боглаев Ю.П. Вычислительная математика и программирование / Ю.П.Боглаев. - М. Высшая школа, 1990. –544с.
2. Марчук Г.И. Методы вычислительной математики / Г.И.Марчук. -М.: Мир, 1989. –375с.
3. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков,Г.М. Кобельков. - М.: Наука, 1987. –487с.
4. Райс Дж. Матричные вычисления и математическое обеспечение / Дж.Райс. - М.: Мир, 1984. –563с.
5. Шуп Т. Решение инженерных задач на ЭВМ / Т.Шуп. - М.: Мир, 1982. –238с.
ПРИЛОЖЕНИЕ А
( обязательно )
Текст программы
program Kursach;
uses crt;
const
{Начальные условия задачи Коши}
t=1;
tf=30; 33333
x0=2;
x1=3.5;
type vektor = array[1..2] of real;
var
f:text;
name:string[20];
E, Emax,et:real;{ошибка в узле,её модуль,максимальная ошибка}
toch,tk,h:real;{точное решение,переменная интегрирования,шаг интегрирования}
x:vektor;
str,n0,n:integer;
{Процедура вычисления правой части}
procedure Right(t:real;var x, f1:vektor);
begin
f1[1]:=x[2]; 33333
f1[2]:=(-2.5*x[2])/t+x[1]/sqr(t);
end;
{Функция вычисления точного решения}
function TochSolve(t:real):real;
begin
TochSolve:=3*exp(0.5*ln(t))-1/sqr(t); точное решение
end;
{RK_2}
procedure RK_2P(t:real;h:real;var x:vektor);
var
xr, f1, f2:vektor;
i:integer;
begin
right(t,x,f1); {1 этап}
for i:=1 to 2 do
xr[i]:=x[i]+2*h/3*f1[i];
right(t,xr,f2); {2 этап}
for i:=1 to 2 do
x[i]:=x[i]+h/4*(f1[i]+3*f2[i]);
end;
{RK_4}
procedure RK_4P(t:real;h:real;var x:vektor);
var
xr,f1,f2,f3,f4:vektor;
h2,h6:real;
i:integer;
begin
h2:=0.5*h;
h6:=0.166666666666*h;
right(t,x,f1); {1 этап}
for i:=1 to 2 do
xr[i]:=x[i]+h2*f1[i];
right(t+h2,xr,f2); {2 этап}
for i:=1 to 2 do
xr[i]:=x[i]+h2*f2[i];
right(t+h2,xr,f3); {3 этап}
for i:=1 to 2 do
xr[i]:=x[i]+h*f3[i];
right(t+h,xr,f4);{4 этап}
for i:=1 to 2 do
x[i]:=x[i]+h6*(f1[i]+2*(f2[i]+f3[i])+f4[i]);
end;
{Вызывающая программма}
begin
clrscr;
write('Введите имя файла:');
readln(name);
assign(f,name);
rewrite(f);
writeln(f, 'Результаты вычислений:');
repeat
write('Введите порядок метода Рунге-Кутты (2 или 4) ->');
read(n);
until (n=2)or(n=4);
clrscr;
writeln ('========Метод Рунге-Кутты ',n,'-го порядка=========');
write('Введите шаг интегрирования: ');
readln(h);
write('Введите шаг вывода на экран и в файл: ');
readln(str);
writeln;
n0:=0;
x[1]:=x0;
x[2]:=x1;
tk:=t;
eMax:=0;
E:=0;
et:=0;
writeln(' tk Точное решение Выч-е решение Ошибка');
writeln(f,' tk Точное реш-е Выч-е реш-е Ошибка');
while tk<tf do
begin
if n=4 then RK_4P(tk,h,x) else RK_2P(tk,h,x);
toch:=TochSolve(tk);
et:=toch-x[1];
E:=abs(et);
if E>EMax then
EMax:=E;
if n0=str then
begin
writeln(tk:3:1,' ',toch:10:5,' ',x[1]:10:5,' ',et:5);
writeln(f,tk:3:1,' ',toch:10:5,' ',x[1]:10:5,' ',et:5);
n0:=0;
end;
if (tf-tk<h) then begin
h:=tf-tk;
tk:=tk+h;
end else
tk:=tk+h;
n0:=n0+1;
end;
if n=2 then RK_2P(tf,h,x) else RK_4P(tf,h,x);
toch:=TochSolve(tk);
et:=toch-x[1];
E:=abs(et);
if E>eMax then
eMax:=E;
writeln(tf:5,' ',toch:10:5,' ',x[1]:10:5,' ',et:5);
writeln(f,tf:5,' ',toch:10:5,' ',x[1]:10:5,' ',et:5);
writeln('Максимальная ошибка, max=',eMax);
writeln(f,'Максимальная ошибка, max=',eMax);
if n=2 then
begin
writeln('Оценка ошибки интегрирования, C=',eMax/sqr(h));
writeln(f,'Оценка ошибки интегрирования, C=',eMax/sqr(h));
end else
begin
writeln('Оценка ошибки интегрирования, C=',eMax/sqr(sqr(h)));
writeln(f,'Оценка ошибки интегрирования, C=',eMax/sqr(sqr(h)));
end;
close(f);
readkey;
end.
ПРИЛОЖЕНИЕ Б
( обязательно )













|





|




























Функция вычисления точного решения ОДУ при текущем t
 |
x(t) =3*t^(0,5) – t^(-2)
Процедура вычисления правой части системы уравнений
 |


|
Рунге – Кутты второго порядка


F1=f(x(tk–1),tk–1)
 |
Вычисление аргумента
правой части для F2

 |
F2=f(xr,tk-2 + h2)
 |
x(tk)=x(tk–1)+h/4(F1+3F2)

 |




















ПРИЛОЖЕНИЕ В
( обязательно )
Результаты работы программы
Метод 2-го порядка:
h=0.001
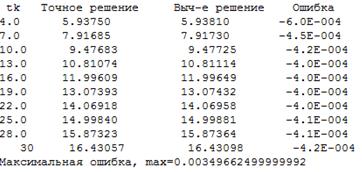
h=0.1

h=1

Метод 4-го порядка:
h=0.001

h=0.1

h=1

