Главная | Обратная связь

Приведення системи лінійних рівнянь до жорданової форми

РІШЕННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ МЕТОДОМ ГАУСА - ЖОРДАНА

Основні поняття

Система m лінійних рівнянь із n невідомими має такий вигляд:

 

Тут х_j ( j=1, n ) – змінні ( або невідомі) системи, а_ij ( i =1,m; j = 1,n ) – коефіцієнти при змінних, в_i ( i =1,m ) – вільні члени.

Рішенням системи ( І.І) називається всякий набір значень змінних х₁, х₂, …, х_n, при якому всі рівняння перетворюються в тотожності. Система називається сумісною, якщо вона має хоча б одне рішення, і несумісною – у протилежному випадку.

Наприклад, система

сумісна, тому що вона має, зокрема, таке рішення:

х₁ = 1; х₂ = 2; х₃ = 0 . Система ж

несумісна.

Дві системи лінійних рівнянь називаються рівносильними, якщо кожне рішення однієї з них є рішенням іншої, і навпаки. Якщо яке-небудь рівняння системи помножити на постійний множник λ ≠ 0 , то вийде система рівнянь, рівносильна вихідній. Аналогічно, якщо до якого-небудь рівняння системи додати інше рівняння системи, то вийде система, рівносильна вихідній.

Нарешті якщо у системі є рівняння виду

0∙ х₁ + 0∙ х₂ + ... + 0∙ х_n = 0, то таке рівняння можна вилучити, одержавши систему, рівносильну вихідній.

 

Приведення системи лінійних рівнянь до жорданової форми

 

Процес відшукування рішення системи лінійних рівнянь починається з того, що система приводиться до жорданової форми.

Визначення. Жордановою формою системи (I.I) називається система лінійних рівнянь, що володіє наступними властивостями:

а) вона рівносильна системі (I.I)

б) у кожному рівнянні жорданової форми є така змінна, котра входить у це рівняння з коефіцієнтом 1, а в інші рівняння - з коефіцієнтом 0.

Так, якщо системі (I.I) рівносильна наступній системі лінійних рівнянь:

 

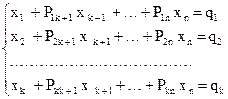(1.2)

то (І.2) є жорданова форма для (I.I). При цьому змінні х_1, х₂,... ,х_к називаються базисними, останні змінні х_к+1,..., х_n називаються вільними. Жорданова форма завжди є сумісною системою лінійних рівнянь. Дійсно, система (І.2) має наступне рішення:

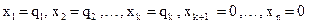(І.3)

Оскільки система (І.2) рівносильна системі ( І.І ) , то (І.3) є рішенням системи (І.І).

Таким чином, якщо для системи лінійних рівнянь ( І.І ) існує жорданова форма, то ( І.І ) - сумісна система. Несумісна система жорданової форми не має.

Покажемо, що будь-яку сумісну систему можна привести до жорданової форми. Це досягається методом Гауса-Жордана, який полягає в наступному.

Розглянемо перше рівняння системи (І.І). Виберемо в ньому змінну, коефіцієнт при якій відмінний від нуля. Припустимо, що а₁₁ ≠ 0. Поділимо рівняння на а₁₁.

Одержимо рівняння

х₁+ а₁₂х₂ + … + а_1nх_n = в₁ (І.4)

 

Будемо змінну х₁ робити базисною в жордановій формі. Для цього її потрібно вилучити з інших рівнянь системи. Щоб вилучити х₁ із другого рівняння, помножимо рівняння (І.4) на -а₂₁ і складемо із другим рівнянням. Потім вилучимо х₁ із третього рівняння, для чого рівняння (І.4) помножимо на -а₃₁ і складемо із третім рівнянням. Аналогічно змінна х₁ вилучається з інших рівнянь. Таким чином, взявши за "ведуче" перше рівняння й провівши серію "жорданових вилучень", ми одержимо рівносильну (I.I) систему рівнянь, уякій x₁ входить у перше рівняння з коефіцієнтом 1 , а вінші рівняння - з коефіцієнтом 0.

Після цього вибираємо як ведуче друге рівняння отриманої системи. У цьому рівнянні беремо коефіцієнт, відмінний від нуля (нехай це коефіцієнт при х₂),ділимо рівняння на цей коефіцієнт і потім виключаємо х₂ із всіх інших рівнянь (у тому числі й з першого). Потім за відуче вибираємо третє рівняння й т.д.

Якщо на деякому кроці виникне рівняння виду

0∙ х₁ + 0∙ х₂ + ... + 0∙ х_n = 0 (І.5)

то вилучаємо його із системи. Якщо ж виникне рівняння виду

0∙ х₁ + 0∙ х₂ + ... + 0∙ х_n = b ≠ 0, то це свідчить про несумісність вихідної системи ( І.І), а несумісна система до жорданової форми не приводиться.

Отже , метод Гауса-Жордана сумісну систему лінійних рівнянь приводить до жорданової форми, а у випадку несумісної системи виявляє несумісність.

Ясно, що вжордановій формі число рівнянь не може бути більше числа рівнянь у вихідній системі. Так, якщо система (1.2) є жордановою формою для системи (I.I), то , причому сувора нерівність має місце тоді, коли на деяких кроках жорданової процедури вилучалися рівняння виду (1.5).

Очевидно, та сама система може мати багато різних жорданових форм.

 

Приклад. Привести до жорданової форми

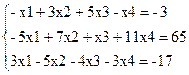
Виберемо як ведуче перше рівняння, а як базисну змінну - змінну х_1. Поділимо перше рівняння на (-1) (коефіцієнт при х₁), одержимо:

Помножимо це рівняння на (+5) і додамо до другого рівняння, потім помножимо його на (-3) і додамо до третього рівняння.

Одержимо систему:

 

Тепер зробимо ведучим друге рівняння, а базисною змінною - змінну 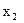. Поділивши друге рівняння на (-8) і виключивши 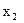з першого й третього рівнянь, одержимо систему:

Нарешті, у третьому рівнянні вибираємо за базисну змінну 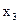. Поділимо це рівняння на (-1) і виключимо 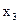з інших рівнянь. Одержимо жорданову форму:

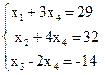
Змінні 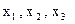є базисними, змінна - вільною.